题目内容
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.

证明:(1)∵E是AD的中点,∴AE=ED.
∵AF∥BC,∴∠AFE=∠DBE, ∠FAE=∠BDE,
∴△AFE≌△DBE.
∴AF=DB.
∵AD是BC边上的中点,∴DB=DC,AF=DC
 (2)四边形ADCF是菱形.
(2)四边形ADCF是菱形.
理由:由(1)知,AF=DC,
∵AF∥CD, ∴四边形ADCF是平行四边形.
又∵AB⊥AC, ∴△ABC是直角三角形
∵AD是BC边上的中线, ∴ .
.
∴平行四边形ADCF是菱形.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

 三个数都是神秘数。
三个数都是神秘数。 数为2k+2和2k(其中k取非负数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么?
数为2k+2和2k(其中k取非负数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么? 么?
么? ,
, ,
, ,
, ,…(
,…( ),其中第7个式子是 ,第
),其中第7个式子是 ,第 个式子是 (
个式子是 ( 为正整数)。
为正整数)。 B.
B.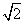 ,
,
 ,
, ,
,
 =____ ___.
=____ ___. )的等腰三角形铁皮,用它烙一块与铁皮形状.大小相同的饼.烙好一面后把饼翻身,这块饼仍能正好落在“锅”中,这是因
)的等腰三角形铁皮,用它烙一块与铁皮形状.大小相同的饼.烙好一面后把饼翻身,这块饼仍能正好落在“锅”中,这是因 为 .
为 .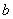 ) 图(
) 图(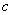 )
) .请你在图(
.请你在图( (
( 的和是
的和是 ,则这个多项式是 .
,则这个多项式是 .