Question

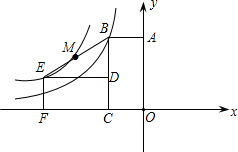
如图，已知矩形ABCD的边BC在x轴上，矩形ABCD对角线的交点E的横坐标为m（m＞0），且点A、E和点N（1，2）都在函数y=

k

x

的图象上．
（1）求k的值；
（2）求点A的坐标（用m表示）；
（3）当满足上述条件的矩形ABCD为正方形时，请求出此时m的值；
（4）点F在y轴的正半轴上，且OF=OB，在（3）的条件下，是否线段BC上存在点P，使PD=PF，若存在，求出符合条件的点P的坐标，若不存在，请说明理由．

Answer 1

（1）因为抛物线过N（1，2），所以k=2；

（2）∵E的横坐标为m（m＞0），
∴纵坐标为

2

m

，根据矩形性质，AB=

4

m

，即A点纵坐标为

4

m

，代入y=

2

x

中，得x=

m

2

，
∴A（

m

2

，

4

m

）；

（3）根据上面的解题过程可得B（

m

2

，0），C（

3

2

m，0），BC=m，
∵AB=BC，∴

4

m

=m，解得m=±2，
∵m＞0，∴m=2；

（4）若PD=PF，则P为DF的垂直平分线与x轴的交点，
根据题意在BC上，设其坐标为P（x，0），则PC=3-x，
根据勾股定理得

x2+12

=

(3-x)2+22

，解得x=2，
∴线段BC上存在点P，使PD=PF，P（2，0）．