题目内容
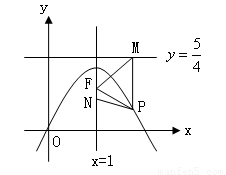
(15分)已知抛物线![]() 顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线
顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线![]() 作垂线,垂足为M,连FM(如图).
作垂线,垂足为M,连FM(如图).
(1)求字母a,b,c的值;
(2)在直线x=1上有一点![]() ,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
(3)对抛物线上任意一点P,是否总存在一点N(1,t),使PM=PN恒成立,若存在请求出t值,若不存在请说明理由.
(1)a=-1,b=2,c=0
(2)略
(3)不存在
解析:(1)a=-1,b=2,c=0
(2)过P作直线x=1的垂线,可求P的纵坐标为![]() ,横坐标为
,横坐标为![]() .此时,MP=MF=PF=1,故△MPF为正三角形.
.此时,MP=MF=PF=1,故△MPF为正三角形.
(3)不存在.因为当t<![]() ,x<1时,PM与PN不可能相等,同理,当t>
,x<1时,PM与PN不可能相等,同理,当t>![]() ,x>1时,PM与PN不可能相等.
,x>1时,PM与PN不可能相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
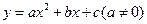 顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线
顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线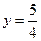 作垂线,垂足为M,连FM(如图).
作垂线,垂足为M,连FM(如图).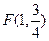 ,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;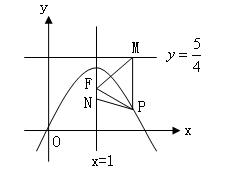
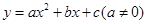 顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线
顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线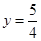 作垂线,垂足为M,连FM(如图).
作垂线,垂足为M,连FM(如图).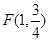 ,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;