��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�MΪx���������ϵ�һ�㣬��M��x�ύ��A��B���㣬��y�ύ��C��D���㣬��A��-1��0����C�������Ϊ(0��
)��

��1����M������ꣻ
��2����ͼ��PΪ
�ϵ�һ�����㣬CQƽ�֡�PCD����P���˶�ʱ���߶�AQ�ij����Ƿ�ı䣿�����䣬������ֵ�����ı䣬�������仯��Χ��

��3����ͼ����AΪԲ��ACΪ�뾶����A��PΪ��A�ϲ�ͬ��C��D��һ�����㣬ֱ��PC����M�ڵ�Q��KΪPQ���е㣬��P���˶�ʱ���ָ����������ۣ���
��ֵ���䣻���߶�OK�ij��Ȳ��䣮��������ֻ��һ��������ȷ��ѡ����ȷ�Ľ���֤��������ֵ��

| 3 |

��1����M������ꣻ
��2����ͼ��PΪ
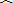 |
| BC |

��3����ͼ����AΪԲ��ACΪ�뾶����A��PΪ��A�ϲ�ͬ��C��D��һ�����㣬ֱ��PC����M�ڵ�Q��KΪPQ���е㣬��P���˶�ʱ���ָ����������ۣ���
| CK |
| PQ |

��1������MC�����M�İ뾶ΪR
��A��-1��0����C��0��
����OC2+OM2=MC2
��(
)2+(R-1)2=R2
���R=2��
��M���������1��0����
��2��AQ���䣬AQ=AC=2��
����AC���ߡ�ACD=��P
�֡�CQƽ�֡�OCP
���PCQ=��OCQ
���ACD+��OCQ=��PCQ+��P
������ACQ=��AQC
��AQ=AC=2��
��3��OK���䣬OK=
��
����PD��QD��KD��
��AC=
=2
���A�İ뾶Ϊ2
�ߡ�A�İ뾶Ϊ2����M�İ뾶Ϊ2
���A����MΪ��Բ
��
=
���DPQ=��DQP
��DQ=DP
��KΪPQ���е�
��DK��PQ
��OC=OD
��OK=
CD=OC=
��

��A��-1��0����C��0��
| 3 |
��(
| 3 |
���R=2��
��M���������1��0����
��2��AQ���䣬AQ=AC=2��

����AC���ߡ�ACD=��P
�֡�CQƽ�֡�OCP
���PCQ=��OCQ
���ACD+��OCQ=��PCQ+��P
������ACQ=��AQC
��AQ=AC=2��
��3��OK���䣬OK=
| 3 |
����PD��QD��KD��

��AC=
(
|
���A�İ뾶Ϊ2
�ߡ�A�İ뾶Ϊ2����M�İ뾶Ϊ2
���A����MΪ��Բ
��
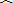 |
| DAC |
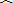 |
| DMC |
���DPQ=��DQP
��DQ=DP
��KΪPQ���е�
��DK��PQ
��OC=OD
��OK=
| 1 |
| 2 |
| 3 |


��ϰ��ϵ�д�
�����Ŀ







