题目内容
(1)计算:
①( -
-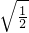 )
)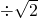 ;
;
②3-2-(π-3)0+ +|
+| -2|.
-2|.
(2)用适当方法解方程:2(x-3)2+x(x-3)=0.
解:(1)原式= ÷
÷ -
-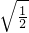 ÷
÷
=2-
= ;
;
(2)原式= -1+2
-1+2 +2-
+2-
=1 +2
+2 -
- ;
;
(3)分解因式得:(x-3)[2(x-3)+x]=0,
(x-3)(3x-6)=0,
x-3=0,3x-6=0,
解得:x1=3,x2=2.
分析:(1)根据多项式除以单项式法则展开,再根据单项式除以单项式进行计算即可;
(2)先根据负整数指数幂、零指数幂、二次根式的性质,绝对值分别计算每一部分的值,再代入后合并即可;
(3)先分解因式得出(x-3)(3x-6)=0,推出x-3=0,3x-6=0,求出方程的解即可.
点评:本题考查了负整数指数幂、零指数幂、二次根式的性质,绝对值,整式的混合运算,解一元二次方程等知识点的综合运用.
 ÷
÷ -
-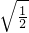 ÷
÷
=2-

=
 ;
;(2)原式=
 -1+2
-1+2 +2-
+2-
=1
 +2
+2 -
- ;
;(3)分解因式得:(x-3)[2(x-3)+x]=0,
(x-3)(3x-6)=0,
x-3=0,3x-6=0,
解得:x1=3,x2=2.
分析:(1)根据多项式除以单项式法则展开,再根据单项式除以单项式进行计算即可;
(2)先根据负整数指数幂、零指数幂、二次根式的性质,绝对值分别计算每一部分的值,再代入后合并即可;
(3)先分解因式得出(x-3)(3x-6)=0,推出x-3=0,3x-6=0,求出方程的解即可.
点评:本题考查了负整数指数幂、零指数幂、二次根式的性质,绝对值,整式的混合运算,解一元二次方程等知识点的综合运用.

练习册系列答案
相关题目
