题目内容
![]() 如图所示,A、B分别是轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.
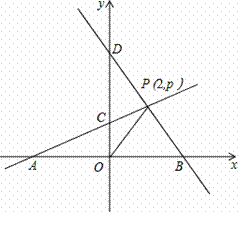
如图所示,A、B分别是轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.
![]() (1)求△COP的面积;
(1)求△COP的面积;
(2)求点A的坐标及p的值;
(3)若△BOP与△DOP的面积相等,求直线BD的函数关系式.
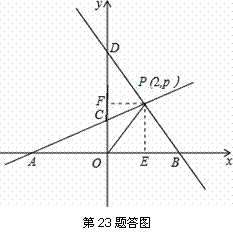
解:(1)过点P作PF⊥y轴于点F,则PF=2.
∵ C(0,2),∴ CO=2.∴ S△COP=×2×2=2.
![]() (2)∵ S△AOP=6,S△COP=2,∴ S△COA=4,∴ OA×2=4,
(2)∵ S△AOP=6,S△COP=2,∴ S△COA=4,∴ OA×2=4,
∴ OA=4,∴ A(-4,0).∴ S△AOP=×4|p|=6,∴ |p|=3.
∵ 点P在第一象限,∴ p=3.
(3)∵ S△BOP=S△DOP,且这两个三角形同高,∴ DP=BP,即P为BD的中点.
作PE⊥轴于点E,则E(2,0),F(0,3).∴ B(4,0),D(0,6).
设直线BD的关系式为y=k+b(k≠0),则解得
∴ 直线BD的函数关系式为y=+6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
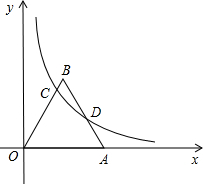 分别交AB、OB于D、C两点,其中D为AB中点
分别交AB、OB于D、C两点,其中D为AB中点
 15、如图所示,这个风铃分别由正三、正四、正五、正六、正八、正十和正十二边形的饰物组成,共重144克,(假设绳子和横杆的重量为0),请你计算出每个正多边形饰物的重量.
15、如图所示,这个风铃分别由正三、正四、正五、正六、正八、正十和正十二边形的饰物组成,共重144克,(假设绳子和横杆的重量为0),请你计算出每个正多边形饰物的重量. (2012•石景山区二模)如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳3×2-2=4步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为
(2012•石景山区二模)如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳3×2-2=4步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 如图所示,下列实物分别接近于什么立体图形?请写在每个图下面的括号内.
如图所示,下列实物分别接近于什么立体图形?请写在每个图下面的括号内.