题目内容
已知线段AB的中点为C，以点A为圆心，AB的长为半径作圆，在线段AB的延长线上取点D，使得BD=AC；再以点D为圆心，DA的长为半径作圆，与⊙A分别相交于F，G两点，连接FG交AB于点H，则| AH | AB |
分析：延长AD与⊙D交于点E，连接AF，EF．由题设知AC=
AD，AB=
AE，又有Rt△FHA∽Rt△EFA，所以
=
．而AF=AB，所以
=
=
．
| 1 |
| 3 |
| 1 |
| 3 |
| AH |
| AF |
| AF |
| AE |
| AH |
| AB |
| AB |
| AE |
| 1 |
| 3 |
解答：
解：如图，延长AD与⊙D交于点E，连接AF，EF．
∵线段AB的中点为C，
∴AC=BC，
∵BD=AC，
∴BD=AC=BC，
∴AC=
AD，
∵AC=
AB，AD=
AE，
∴AB=
AE，
在△FHA和△EFA中，
∵∠EFA=∠FHA=90°，∠FAH=∠EAF，
∴Rt△FHA∽Rt△EFA，
∴
=
，
∵AF=AB，
∴
=
=
．
故答案为：
．
解：如图，延长AD与⊙D交于点E，连接AF，EF．∵线段AB的中点为C，
∴AC=BC，
∵BD=AC，
∴BD=AC=BC，
∴AC=
| 1 |
| 3 |
∵AC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| 1 |
| 3 |
在△FHA和△EFA中，
∵∠EFA=∠FHA=90°，∠FAH=∠EAF，
∴Rt△FHA∽Rt△EFA，
∴
| AH |
| AF |
| AF |
| AE |
∵AF=AB，
∴
| AH |
| AB |
| AB |
| AE |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：此题主要考查了相似三角形的判定和性质，注意相等线段之间的等量代换．
练习册系列答案
阅读快车系列答案
相关题目
已知线段AB的中点为C，以点A为圆心，AB的长为半径作圆，在线段AB的延长线上取点D，使得BD=AC；再以点D为圆心，DA的长为半径作圆，与⊙A分别相交于F，G两点，连接FG交AB于点H，则
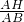的值为________．
的值为 ．
的值为 ．