题目内容
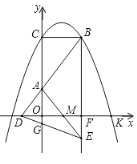
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
【答案】(1)BC=m;(2)点D在抛物线上,理由见解析; (3)![]() .
.
【解析】
(1)先求出抛物线的对称轴,然后根据点C与点B关于对称轴对称即可求出BC的长;
(2)根据题意即可求出BC和二次函数解析式,根据利用平行证出△AOD∽△ACB,列出比例式即可求出点D的坐标,最后代入解析式即可判断结论;
(3)根据已知条件可得点E的坐标为(m,![]() ),即OF=m,EF=
),即OF=m,EF=![]() ,△ODG∽△FDE,然后用m表示出OD、DF、OG、MF和OM,再利用平行证出△AOM∽△EFM,列出比例式即可求出m的值,从而求出结论.
,△ODG∽△FDE,然后用m表示出OD、DF、OG、MF和OM,再利用平行证出△AOM∽△EFM,列出比例式即可求出m的值,从而求出结论.
解:(1)![]() 图象的对称轴为直线x=
图象的对称轴为直线x=![]() ,点C与点B关于对称轴对称
,点C与点B关于对称轴对称
∴BC=![]() =m;
=m;
(2)在,理由如下
当m=2时,BC=2,![]()
∵![]() ,
,![]()
∴△AOD∽△ACB
∴![]()
∴OD=![]() BC=1
BC=1
∴点D的坐标为(-1,0)
当x=-1时,![]()
∴点D在抛物线.
(3)∵![]() ,
,![]()
∴点E的坐标为(m,![]() ),即OF=m,EF=
),即OF=m,EF=![]() ,△ODG∽△FDE
,△ODG∽△FDE
由(2)可知![]()
∴OD=![]() BC=
BC=![]() m,OA=
m,OA=![]() OC
OC
∴DF=OD+OF=![]() m
m
∴![]()
即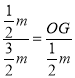
解得:OG=![]() m
m
∵![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]()
∴![]() EF·MF=2×
EF·MF=2×![]() OD·OG
OD·OG
即![]() ·
·![]() ·MF=2×
·MF=2×![]() ·
·![]() m·
m·![]() m
m
解得:MF=![]() m
m
∴OM=OF-MF=![]() m
m
将x=0代入![]() 中,解得y=3
中,解得y=3
∴OC=3
∴OA=1
∵OA∥EF
∴△AOM∽△EFM
∴![]()
即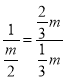
解得:m=1
∴抛物线的解析式为![]()

 优等生题库系列答案
优等生题库系列答案【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,长沙市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大;并求出最大利润.