题目内容
如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
(1)在图1中,写出∠A、∠B、∠C、∠D之间关系为;
(2)如图2,在(1)的结论下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.
①仔细观察,在图2中有
②若∠D=40°,∠B=36°,试求∠P的度数;
③∠D和∠B为任意角时,其他条件不变,试直接写出∠P与∠D、∠B之间数量关系,不需说明理由.
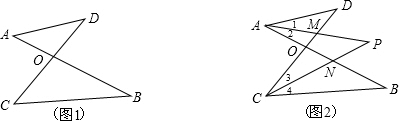
(1)在图1中,写出∠A、∠B、∠C、∠D之间关系为;
(2)如图2,在(1)的结论下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.
①仔细观察,在图2中有
6
6
个以线段AD为边的“8字形”;②若∠D=40°,∠B=36°,试求∠P的度数;
③∠D和∠B为任意角时,其他条件不变,试直接写出∠P与∠D、∠B之间数量关系,不需说明理由.
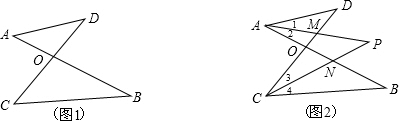
分析:(1)根据三角形内角和定理得到∠A+∠D+∠AOD=180°,∠C+∠D+∠BOC=180°,根据对顶角相等得∠AOD=∠BOC,所以∠A+∠D=∠B+∠C;
(2)①以M为交点的“8字形”有1个,以N为交点的“8字形”有1个,以O为交点的“8字形”有4个;
②根据角平分线的定义得到∠1=∠2,∠3=∠4,再根据(1)中的结论得到∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,两等式相减得到∠D-∠P=∠P-∠B,
即∠P=
(∠D+∠B),然后把∠D=40°,∠B=36°代入计算即可;
③由②的证明得到∠P=
(∠D+∠B).
(2)①以M为交点的“8字形”有1个,以N为交点的“8字形”有1个,以O为交点的“8字形”有4个;
②根据角平分线的定义得到∠1=∠2,∠3=∠4,再根据(1)中的结论得到∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,两等式相减得到∠D-∠P=∠P-∠B,
即∠P=
| 1 |
| 2 |
③由②的证明得到∠P=
| 1 |
| 2 |
解答:解:(1)∵∠A+∠D+∠AOD=180°,∠C+∠D+∠BOC=180°,
而∠AOD=∠BOC,
∴∠A+∠D=∠B+∠C;
(2)①6;
②∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠1=∠2,∠3=∠4,
∵∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠D-∠P=∠P-∠B,
即∠P=
(∠D+∠B),
∵∠D=40°,∠B=36°
∴∠P=
(40°+36°)=38°;
(4)∠P=
(∠B+∠D).
故答案为6.
而∠AOD=∠BOC,
∴∠A+∠D=∠B+∠C;
(2)①6;
②∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠1=∠2,∠3=∠4,
∵∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠D-∠P=∠P-∠B,
即∠P=
| 1 |
| 2 |
∵∠D=40°,∠B=36°
∴∠P=
| 1 |
| 2 |
(4)∠P=
| 1 |
| 2 |
故答案为6.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线的定义.

练习册系列答案
相关题目




