题目内容
 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则△ABC面积为
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则△ABC面积为
- A.13
- B.12
- C.6.5
- D.6
C
分析:过B作EF⊥直线l1于E,交直线l3于F,则BE=2,BF=3,证△CEB≌△BFA,推出CE=BF=3,BE=FA=2,由勾股定理求出AB、BC,根据三角形面积公式求出即可.
解答: 解:过B作EF⊥直线l1于E,交直线l3于F,
解:过B作EF⊥直线l1于E,交直线l3于F,
∵l1∥l2∥l3,
∴EF⊥l3,
则BE=2,BF=3,
∴∠CEB=∠AFB=90°=∠CBA,
∴∠ECB+∠EBC=90°,∠EBC+∠ABF=90°,
∴∠ECB=∠ABF,
在△CEB和△BFA中,
 ,
,
∴△CEB≌△BFA(AAS),
∴CE=BF=3,BE=FA=2,
由勾股定理得:AB=BC= =
= ,
,
∴△ABC面积为 BC×AC=
BC×AC= ×
× ×
× =6.5,
=6.5,
故选C.
点评:本题考查了勾股定理,三角形面积公式,全等三角形的性质和判定的应用,关键是求出AB、BC的长.
分析:过B作EF⊥直线l1于E,交直线l3于F,则BE=2,BF=3,证△CEB≌△BFA,推出CE=BF=3,BE=FA=2,由勾股定理求出AB、BC,根据三角形面积公式求出即可.
解答:
 解:过B作EF⊥直线l1于E,交直线l3于F,
解:过B作EF⊥直线l1于E,交直线l3于F,∵l1∥l2∥l3,
∴EF⊥l3,
则BE=2,BF=3,
∴∠CEB=∠AFB=90°=∠CBA,
∴∠ECB+∠EBC=90°,∠EBC+∠ABF=90°,
∴∠ECB=∠ABF,
在△CEB和△BFA中,
 ,
,∴△CEB≌△BFA(AAS),
∴CE=BF=3,BE=FA=2,
由勾股定理得:AB=BC=
 =
= ,
,∴△ABC面积为
 BC×AC=
BC×AC= ×
× ×
× =6.5,
=6.5,故选C.
点评:本题考查了勾股定理,三角形面积公式,全等三角形的性质和判定的应用,关键是求出AB、BC的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.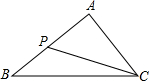 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )