题目内容
如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别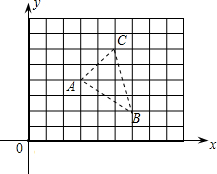 为(3,4)、(6,2)、(5,6).
为(3,4)、(6,2)、(5,6).(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求此平行四边形的周长.
分析:(1)根据点的位置和平行四边形的判定即可求出D的坐标;
(2)根据点的坐标和勾股定理即可求出AB、AC、CB的长,再利用平行四边形的性质就能求出平行四边形的周长.
(2)根据点的坐标和勾股定理即可求出AB、AC、CB的长,再利用平行四边形的性质就能求出平行四边形的周长.
解答:解:(1)D点的坐标是(4,0),(8,4),(2,8).
(2)当D点的坐标是(4,0)时,由勾股定理得:
AD=
=
,
AC=
=2
,
∴平行四边形ADBC的周长是2(
+2
)=2
+4
;
当D点的坐标是(8,4)时,同法可求:
AB=
,
∵AC=2
,
∴平行四边形ABDC的周长是2(
+2
)=2
+4
当D点的坐标是(2,8)时,同法可求:
CB=
,
∴平行四边形ABCD的周长是2(
+
)=2
+2
.
答:平行四边形的周长是2
+4
或2
+4
或2
+2
.
(2)当D点的坐标是(4,0)时,由勾股定理得:
AD=
| (4-3)2+42 |
| 17 |
AC=
| (5-3)2+(5-3)2 |
| 2 |
∴平行四边形ADBC的周长是2(
| 17 |
| 2 |
| 17 |
| 2 |
当D点的坐标是(8,4)时,同法可求:
AB=
| 13 |
∵AC=2
| 2 |
∴平行四边形ABDC的周长是2(
| 13 |
| 2 |
| 13 |
| 2 |
当D点的坐标是(2,8)时,同法可求:
CB=
| 17 |
∴平行四边形ABCD的周长是2(
| 13 |
| 17 |
| 13 |
| 17 |
答:平行四边形的周长是2
| 17 |
| 2 |
| 13 |
| 2 |
| 13 |
| 17 |
点评:本题主要考查了平行四边形的性质和判定,坐标与图形性质,勾股定理等知识点解此题的关键是求各线段的长.用的数学思想是分类讨论思想.

练习册系列答案
相关题目
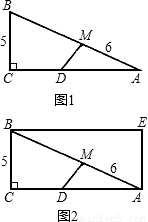
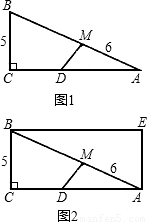
 如图1,Rt△ABC中,∠C=90°,AC=12,BC=5,点M在边AB上,且AM=6.
如图1,Rt△ABC中,∠C=90°,AC=12,BC=5,点M在边AB上,且AM=6.
 (2012•虹口区一模)如图,某商场开业,要为一段楼梯铺上红地毯,已知楼梯高AB=6m,坡面AC的坡度i=1:
(2012•虹口区一模)如图,某商场开业,要为一段楼梯铺上红地毯,已知楼梯高AB=6m,坡面AC的坡度i=1: