题目内容
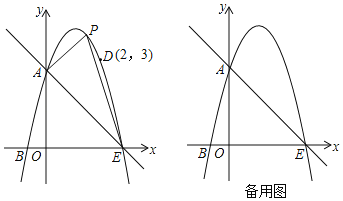
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,以点
,以点![]() 为直角项点,
为直角项点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,再过点
,再过点![]() 作
作![]() ,分别交直线
,分别交直线![]() 和
和![]() 轴于
轴于![]() ,
,![]() 两点,以点
两点,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,…,按此规律进行下去,则点
,…,按此规律进行下去,则点![]() 的坐标为__________ (结果用含正整数
的坐标为__________ (结果用含正整数![]() 的代数式表示).
的代数式表示).

【答案】![]()
【解析】
先根据点A1的坐标以及A1B1∥y轴,求得B1的坐标,进而根据等腰直角三角形的性质得到B2的坐标,即可求得A2的坐标,从而求得C1的坐标,进而得到B3的坐标,求得A3的坐标,从而求得C2的坐标,最后根据根据变换规律,求得Cn的坐标.
解:∵点A1(2,1)在直线y=kx上,
∴1=2k,解得k=![]() ,
,
∴直线为y=![]() x,
x,
∵过点A1作A1B1∥y轴交x轴于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,
∴A1C1∥x轴,
∴B2(3,0),C1(3,1),
当x=3时,y=![]() x=
x=![]() ,即A2(2,
,即A2(2,![]() ),
),
∴B3(![]() ,0),
,0),
∴C2(![]() ,
,![]() ),
),
∴以此类推,
C3(![]() ,
,![]() ),
),
…
![]()
![]() ,
,
故答案为:![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
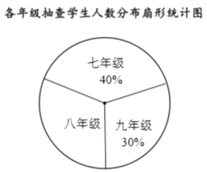
【题目】某初中为了了解学生的视力情况,从三个年级随机抽取了部分学生进行调查,并制作了下面的统计表和统计图.
各年级抽查学生视力各等第人数分布统计表
优秀 | 良好 | 合格 | 不合格 | |
七年级 |
| 20 | 22 | 23 |
八年级 | 11 | 17 | 13 | 19 |
九年级 | 8 |
| 11 | 25 |
(1)在统计表中,![]() ________,
________,![]() ________;
________;
(2)在扇形统计图中,八年级所对应的扇形圆心角为________°;
(3)若该校三个年级共有1800名学生,试估计该校学生视力等第不合格的人数.