Question

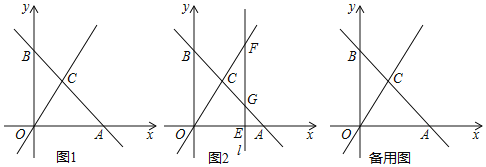
【题目】如图1，平面直角坐标系中，直线与直线交与点．

轴上是否存在点P，使的面积是面积的二倍？若存在，直接写出点P的坐标；若不存在，说明理由．

如图2，若点E是x轴上的一个动点，点E的横坐标为，过点E作直线轴于点E，交直线于点F，交直线于点G，求m为何值时，≌？请说明理由．

在的前提条件下，直线l上是否存在点Q，使的值最小？若存在，直接写出点Q的坐标；若不存在，说明理由．

Answer 1

【答案】(1)见解析;(2)见解析;(3)见解析.

【解析】

利用一次函数图象上点的坐标特征可求出点A的坐标，由和等高且的面积是面积的二倍，可得出，进而可得出点P的坐标；

由可得出∽，利用一次函数图象上点的坐标特征可求出点B的坐标，若要≌，只需，即点C为线段BG的中点，结合点B，C的坐标可得出点G的坐标，再由轴可得出m的值；

作点O关于直线l对称的对称点D，连接BD，交直线l于点Q，此时的值最小，由点O的坐标及直线l的解析式可得出点D的坐标，由点B，D的坐标，利用待定系数法求出直线BD的解析式，再利用一次函数图象上点的坐标特征即可求出点Q的坐标．

解：当时，，
解得：，
点A的坐标为，．
和等高，且的面积是面积的二倍，
，
点P的坐标为或．
，
，，
∽．
当时，，
点B的坐标为．
若要≌，只需．
点B的坐标为，点C的坐标为，
点G的坐标为．
又轴，
．
当时，≌．
由可知，直线l的解析式为，作点O关于直线l对称的对称点D，连接BD，交直线l于点Q，如图3所示．

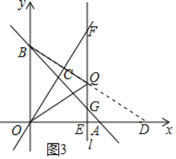
点O，D关于直线l对称，
，点D的坐标为．
，Q，D共线，
此时取得最小值．
设直线BD的解析式为，
将，代入，得：，
解得：，
直线BD的解析式为．
当时，，
直线l上存在点Q，使的值最小，点Q的坐标为．