Question

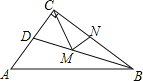
【题目】如图，在Rt△ABC 中，∠ACB＝90°,AC＝80，BC＝60， 点D 从点 B 出发，在线段 BA 上以每秒 4 个单位长度的速度向终点A 运动，连结CD. 设点D 运动的时间为 t 秒.

（1）用含 t 的代数式表示 BD 的长.

（2）求AB 的长及 AB 边上的高.

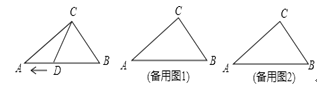
（3）当△BCD 为等腰三角形时，直接写出 t 的值.

Answer 1

【答案】（1）4t；（2）100，48；（3）15秒或18秒或12.5秒

【解析】

（1）根据路程=速度×时间即可解答；

（2）根据勾股定理可求出AB的长，利用等积法可求出AB 边上的高；

（3）分三种情况求解即可.

解：（1）由题意得，BD=4t；

（2）作CH⊥AB于H.

∵∠ACB＝90°,AC＝80，BC＝60，

∴AB=；

∵,

∴100CH=4800,

∴CH=48；

（3）当BC=BD时，

4t=60，

t=15；

当BC=CD时，

∵CH⊥AB，

∴DH=BH.

∵BH=，

∴DH=4t-36，

∴4t-36=36，

∴t=18；

当CD=BD时，

∵CD==，

∴=4t，

解之得

t=12.5.

∴当t=15秒或18秒或12.5秒时，△BCD 为等腰三角形.