Question

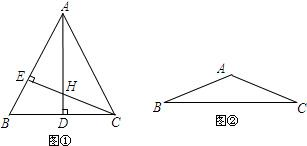22、在△ABC中，AB=AC，AD和CE是高，它们所在的直线相交于H．
（1）若∠BAC=45°（如图①），求证：AH=2BD；
（2）若∠BAC=135°（如图②），（1）中的结论是否依然成立？请在图②中画出图形并证明你的结论．

Answer 1

分析：（1）已知AB=AC，AD⊥BC，推出BC=2BD，继而推出∠EAH=ECB，可证得△AEH≌△CEB．
（2）证明∠ACE=∠CAE=45°，可推出Rt△BEC≌Rt△HEA，继而求证．

解答：证明：（1）∵AB=AC，AD⊥BC，
∴BC=2BD．
∵CE⊥AB，∠BAC=45°，
∴∠ECA=45°．
∴AE=CE．
又AD⊥BC，CE⊥AB，
可得∠EAH=∠ECB．
∴Rt△AEH≌Rt△CEB．
∴AH=BC．
∴AH=2BD．

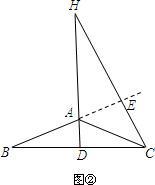（2）答：（1）中结论依然成立．
所画图形如图所示．延长BA交HC于E．
∵∠BAC=135°，
∴∠CAE=45°．
∵AE⊥HC，
∴∠ACE=∠CAE=45°．
∴AE=CE．
∵HD⊥BC，BE⊥HC，
可得∠B=∠H．
∴Rt△BEC≌Rt△HEA．
∴AH=BC．
又BC=2BD，
∴AH=2BD．

点评：本题重点考查了三角形全等的判定定理及等腰三角形的性质；辅助线的作出是解答本题的关键．