题目内容
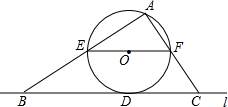 (2013•陕西)如图,直线l与⊙O相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF,并分别延长交直线l于B、C两点.
(2013•陕西)如图,直线l与⊙O相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF,并分别延长交直线l于B、C两点.(1)求证:∠ABC+∠ACB=90°;
(2)当⊙O的半径R=5,BD=12时,求tan∠ACB的值.
分析:(1)由题意可知EF是圆的直径,所以∠EAF=90°,即∠ABC+∠ACB=90°;
(2)连接OD,则OD⊥BD,过E作EH⊥BC于H,则四边形EODH是正方形,易求tan∠BEH=
=
,再证明∠ACB=∠BEH即可.
(2)连接OD,则OD⊥BD,过E作EH⊥BC于H,则四边形EODH是正方形,易求tan∠BEH=
| BH |
| EH |
| 7 |
| 5 |
解答:(1)证明:∵EF是圆的直径,
∴∠EAF=90°,
∴∠ABC+∠ACB=90°;
(2)解:连接OD,则OD⊥BD,
过E作EH⊥BC于H,
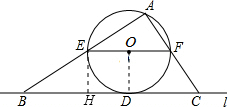
∴EH∥OD,
又∵EO∥HD,OE∥DH,
∴四边形OEHD是矩形,
又∵OE=HD,
∴四边形EODH是正方形,
∴EH=HD=OD=5,
又∵BD=12,
∴BH=7,
在Rt△BEH中,tan∠BEH=
=
,
∵∠ABC+∠BEH=90°,∠ABC+∠ACB=90°,
∴∠ACB=∠BEH,
∴tan∠ACB=
.
∴∠EAF=90°,
∴∠ABC+∠ACB=90°;
(2)解:连接OD,则OD⊥BD,
过E作EH⊥BC于H,

∴EH∥OD,
又∵EO∥HD,OE∥DH,
∴四边形OEHD是矩形,
又∵OE=HD,
∴四边形EODH是正方形,
∴EH=HD=OD=5,
又∵BD=12,
∴BH=7,
在Rt△BEH中,tan∠BEH=
| BH |
| EH |
| 7 |
| 5 |
∵∠ABC+∠BEH=90°,∠ABC+∠ACB=90°,
∴∠ACB=∠BEH,
∴tan∠ACB=
| 7 |
| 5 |
点评:本题考查了圆周角定理、正方形的判定和性质、切线的性质以及锐角三角函数值,题目的综合性很强,难度中等.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 (2013•陕西)如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( )
(2013•陕西)如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( ) (2013•陕西)如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为( )
(2013•陕西)如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为( ) (2013•陕西)如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )
(2013•陕西)如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )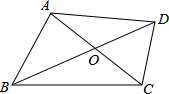 (2013•陕西)如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为
(2013•陕西)如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为 (2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为
(2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为