Question

【题目】在平面直角坐标中，抛物线y=ax2﹣3ax﹣10a（a＞0）分别交x轴于点A、B（点A在点B左侧），交y轴于点C，且OB=OC．

（1）求a的值；

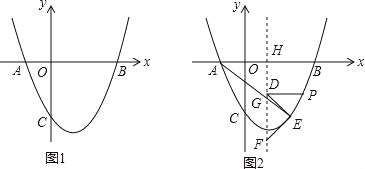
（2）如图1，点P位抛物线上一动点，设点P的横坐标为t（t＞0），连接AC、PA、PC，△PAC的面积为S，求S与t之间的函数关系式；

（3）如图2，在（2）的条件下，设对称轴l交x轴于点H，过P点作PD⊥l，垂足为D，在抛物线、对称轴上分别取点E、F，连接DE、EF，使PD=DE=EF，连接AE交对称轴于点G，直线y=kx﹣k（k≠0）恰好经过点G，将直线y=kx﹣k沿过点H的直线折叠得到对称直线m，直线m恰好经过点A，直线m与第四象限的抛物线交于另一点Q，若=，求点Q的坐标．

Answer 1

【答案】（1）a=；（2）S= t2+t；（3）Q（，﹣）．

【解析】

试题分析：（1）令y=0，求出x轴交点坐标，再用OB=OC求出C点坐标，代入抛物线方程即可；（2）先求出直线AC解析式，再用t表示出PN代入面积公式计算即可；（3）依次求出直线AE的解析式为y=﹣x﹣2，直线WG的解析式为y=3x﹣8，直线KH的解析式为y=﹣2x+3，直线AV的解析式为y=﹣x﹣，即可．

试题解析：（1）令y=0，则ax2﹣3ax﹣10a=0，

即a（x+2）（x﹣5）=0，

∴x1=﹣2，x2=5，

∴A（﹣2，0），B（5，0），

∴OB=5，

∵OB=OC，

∴OC=5，

∴C（0，﹣5），

∴﹣5=﹣10a，

∴a=；

（2）如图1，

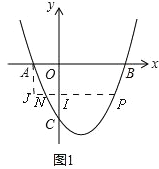
由（1）可知知抛物线解析式为y=x2﹣x﹣5，

设直线AC的解析式为：y=k1x+b，把A、C两点坐标代入得：

，解得：，

∴y=﹣x﹣5，

∵点P的横坐标为t，则P（t， t2﹣t﹣5），

过点P作PN∥x轴交AC于点N，

把y=x2﹣x﹣5，代入直线AC解析式y=﹣x﹣5中，

解得xN=﹣t2+t，

∴N（﹣t2+t， t2﹣t﹣5），

∴PN=t﹣（﹣t2+t）=t2+t，

S=S△ANP+S△CNP=PN×AJ+PN×AI

=PN×OI+PN×CI

=PN（OI+CI）

=PN×OC

=t2+t，

（3）由y=x2﹣x﹣5=（x﹣）2﹣，

得抛物线的对称轴为直线x=，顶点坐标为（，﹣），

∵，

∴设DP=5n，DF=8n，

∵DE=EP=5n，过点E作EM⊥l于点M，则DM=FM=DF=4n，

∴在Rt△DME中，EM=3n，

∴点P的横坐标为5n+，点E横坐标为3n+，

∴yP=（5n+﹣）2﹣=n2﹣，

yE=（3n+﹣）2﹣=n2﹣

∴D（， n2﹣），M（， n2﹣），

∴DM=n2﹣﹣（n2﹣）=8n2，

∴8n2=4n，

∴n=，

∴E（3，﹣5），

∵A（﹣2，0），E（3，﹣5），

∴直线AE的解析式为y=﹣x﹣2，

令x=，则y=﹣x﹣2=﹣﹣2=﹣，

∴G（，﹣），

∵直线y=kx﹣k（k≠0）恰好经过点G，

∴﹣=k﹣k，

∴k=3，

∴直线WG的解析式为y=3x﹣8，

如图2，

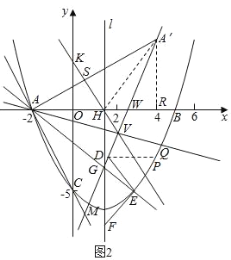
点A关于HK的对称点A′（m，3m﹣8），

∵A（﹣2，0），H（，0），

∴AH=，

∵HS垂直平分AA′，

∴A′H=AH=，

过A′作A′R⊥x轴于R，

在Rt△A′HR中，A′R2+HR2=A′H2，

∴（3m﹣8）2+（m﹣）2=，

∴m1=（舍），m2=，

∴A′（，），

∴tan∠A′AR=，

∵∠HAS+∠AHS=∠OKH+∠AHS=90°，

∴tan∠OKH=tan∠A′AR=，

∴tan∠OKH=，

∴OK=3，

∴K（0，3），

∴直线KH的解析式为y=﹣2x+3，

∵，

∴，

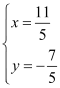∴V（，﹣），

∵A（﹣2，0），

∴直线AV的解析式为y=﹣x﹣，

设Q（s， s2﹣s﹣5），代入y=﹣x﹣中，

s2﹣s﹣5=﹣s﹣，

∴s1=﹣2（舍），s2=，

∴Q（，﹣）．