题目内容
20、如图，在五边形ABCDE中，∠B=∠E，∠C=∠D，BC=DE，M为CD中点，求证：AM⊥CD．分析：证明∠AMC=90°或应用等腰三角形“三线合一”的性质，通过作辅助线将五边形问题恰当地转化为三角形问题是解本例的关键．
解答：
证明：双向延长CD与AB、AE的延长线交于G、H，
则可证△BCG≌△EDH，则BG=EH，∠G=∠H，GC=DH，
∴AG=AH，GM=MH，
又可证△AGM≌△AHM，则∠AMG=∠AMH=90°，
故AM⊥CD．
证明：双向延长CD与AB、AE的延长线交于G、H，则可证△BCG≌△EDH，则BG=EH，∠G=∠H，GC=DH，
∴AG=AH，GM=MH，
又可证△AGM≌△AHM，则∠AMG=∠AMH=90°，
故AM⊥CD．
点评：本题主要考查了全等三角形的判定及性质问题，应熟练掌握．
练习册系列答案
相关题目
7、如图，在五边形ABCDE中，BC∥AD，BD∥AE，AB∥EC．图中与△ABC面积相等的三角形有（ ）
如图，在五边形ABCDE中，∠ABC=∠AED=90°，M是CD的中点，BM=EM，求证：∠BAC=∠EAD．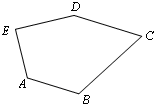
19、如图，在五边形ABCDE中，AE⊥DE，∠BAE=120°，∠BCD=60°，∠CDE-∠ABC=30°．
如图：在五边形ABCDE中，∠ABC=∠AED=90°，∠BAC=∠EAD，M是CD中点，试判断
点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AC上．设点P的运动时间为t（s）．