Question

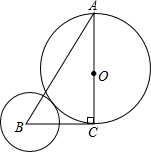已知：如图，在△ABC中，∠C=90°，AC=16，BC=6，AC为⊙O的直径，⊙B的半径长为r．
（1）当r=2时，求证：⊙O与⊙B外切．
（2）求当⊙B与⊙O内切时r的值．

Answer 1

分析：（1）如图，连接BO．欲证明⊙O与⊙B外切，只需证得BO=r+OC即可；
（2）两圆内切时，圆心距=两圆半径之差．

解答：（1）证明：如图，连接BO．
∵AC=16，∴OC=8．
∴BO=

BC2+OC2

=

62+82

=10．
当 r=2时，有 BO=2+OC=2+8=10，
所以，⊙O与⊙B外切；

（2）解：由|r-8|=10，得  
r-8=±10，
解得，r₁=18，r₂=-2（舍去），
所以，当r=18时，⊙O与⊙B内切．

点评：本题考查了勾股定理的应用．解题时，需要弄清楚：两圆内切时，圆心距=两圆半径之差；两圆外切时，圆心距=两圆半径之和．