Question

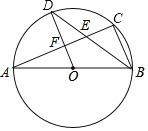
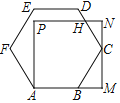
【题目】如图，边长为4的正六边形ABCDEF的顶点B、C分别在正方形AMNP的边AM、MN上，CD与PN交于点H，则HN的长为_____

Answer 1

【答案】

【解析】

在中，根据条件AB=BC=4，∠CBM=60°，∠M=90°，解直角三角形即可解决问题．

∵四边形AMNP是正方形，

∴∠M=90°，

在中，

∵AB=BC=4，∠CBM=60°，∠M=90°，

∴∠BCM=30°，

∴BM=BC=2，CM=BM=2，

∴AM=4+2=6，

∵四边形AMNP是正方形，

∴MN=MA=6，

∴CN=MN﹣CM=6﹣2，

正六边形ABCDEF中，∠BCD=120°，

∴∠HCN=30°，

∵∠M=∠N=90°，

∴△BMC∽△HNC，

∴，

∴，

∴HN=2﹣2，

故答案为：．