题目内容
 在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E、F分别是AC,BC边上一点,且CE=
在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E、F分别是AC,BC边上一点,且CE= AC,BF=
AC,BF= BC,
BC,
(1)求证: ;
;
(2)求∠EDF的度数.
(1)证明:∵CD⊥AB,
∴∠CDB=∠ADC=90°,
∴∠ACD+∠BCD=90°,
∵∠ACB=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∴△ADC∽△CDB,
∴ =
=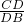 ;
;
(2) 解:∵CE=
解:∵CE= AC,BF=
AC,BF= BC,
BC,
∴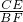 =
= =
= =
=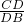 ,
,
又∵∠A=∠BCD,
∴∠ACD=∠B,
∴△CED∽△BFD,
∴∠CDE=∠BDF,
∴∠EDF=∠EDC+∠CDF=∠BDF+∠CDF=∠CDB=90°.
分析:(1)证相关线段所在的三角形相似即可,即证Rt△ADC∽Rt△CDB;
(2)易证得CE:BF=AC:BC,联立(1)的结论,即可得出CE:BF=CD:BD,由此易证得△CED∽△BFD,即可得出∠CDE=∠BDF,由于∠BDF和∠CDF互余,则∠EDC和∠CDF也互余,由此可求得∠EDF的度数.
点评:此题考查的是相似三角形的判定和性质;识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.
∴∠CDB=∠ADC=90°,
∴∠ACD+∠BCD=90°,
∵∠ACB=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∴△ADC∽△CDB,
∴
 =
=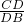 ;
;(2)
 解:∵CE=
解:∵CE= AC,BF=
AC,BF= BC,
BC,∴
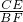 =
= =
= =
=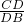 ,
,又∵∠A=∠BCD,
∴∠ACD=∠B,
∴△CED∽△BFD,
∴∠CDE=∠BDF,
∴∠EDF=∠EDC+∠CDF=∠BDF+∠CDF=∠CDB=90°.
分析:(1)证相关线段所在的三角形相似即可,即证Rt△ADC∽Rt△CDB;
(2)易证得CE:BF=AC:BC,联立(1)的结论,即可得出CE:BF=CD:BD,由此易证得△CED∽△BFD,即可得出∠CDE=∠BDF,由于∠BDF和∠CDF互余,则∠EDC和∠CDF也互余,由此可求得∠EDF的度数.
点评:此题考查的是相似三角形的判定和性质;识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.

练习册系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )