题目内容
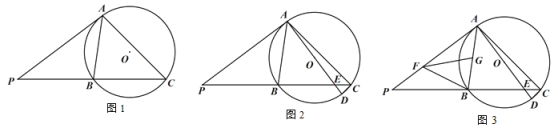
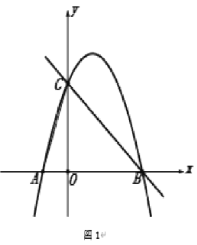
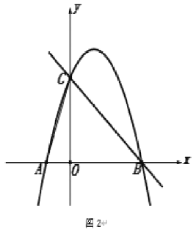
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求抛物线的解析式;
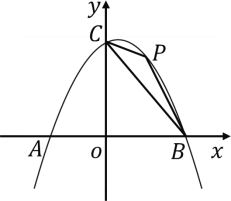
(2)如图2,![]() 为第一象限内抛物线上一点,
为第一象限内抛物线上一点,![]() 的面积为3时,且
的面积为3时,且![]() ,求
,求![]() 点坐标;
点坐标;
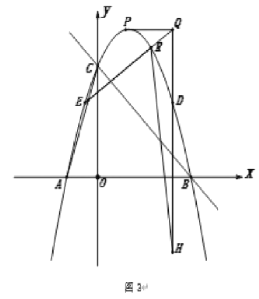
(3)如图3,在(2)的条件下,![]() 、
、![]() 为抛物线上的点,且两点关于抛物线对称轴对称,过
为抛物线上的点,且两点关于抛物线对称轴对称,过![]() 作
作![]() 轴垂线交过点
轴垂线交过点![]() 且平行于
且平行于![]() 轴的直线于
轴的直线于![]() ,
,![]() 交抛物线于
交抛物线于![]() ,延长
,延长![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,当线段
,当线段![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出点C的坐标,利用待定系数法即可解决问题;
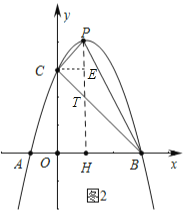
(2)如图2中,作PH⊥AB于H,交BC于T.,作CE⊥PH于E,设P(![]() ,
,![]() ).构建方程即可解决问题;
).构建方程即可解决问题;
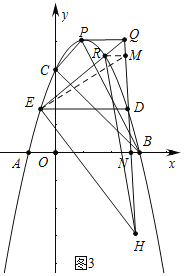
(3)如图3中,作RM⊥DQ于M,连接EM.DH交AB于N.设D(n,![]() ).首先证明△EDQ∽△HDE,推出∠HEQ=90°,由∠REH+∠RMH=180°,推出E、H、M、R四点共圆,推出∠ERH=∠EMH,推出tan∠ERH=tan∠EMD=
).首先证明△EDQ∽△HDE,推出∠HEQ=90°,由∠REH+∠RMH=180°,推出E、H、M、R四点共圆,推出∠ERH=∠EMH,推出tan∠ERH=tan∠EMD=![]() ,推出DM=
,推出DM=![]() (n-1),推出QM=
(n-1),推出QM=![]() ,由RM∥DE,可得
,由RM∥DE,可得![]() ,推出RM=
,推出RM=![]() ,可得点R的坐标
,可得点R的坐标![]() ,把点R坐标代入
,把点R坐标代入![]() ,转化为方程解决问题即可.
,转化为方程解决问题即可.
(1)对于抛物线![]() ,
,
令y=0,得到![]() ,解得
,解得![]() 或3,
或3,
∴A(-1,0),B(3,0),
∴OB=3,
∵∠ABC=45°,
∴OC=OB=3,
∴C(0,3),把(0,3)代入![]() 得到
得到![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)如图2中,作PH⊥AB于H,交BC于T,作CE⊥PH于E,设P(![]() ,
,![]() ).
).
∵B(3,0),C(0,3),
设直线BC的解析式为![]() ,
,
把B(3,0)代入得:![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为![]() ,
,
∴T![]() ,
,
∵![]()
![]()
![]() ,
,
整理得:![]() ,
,
∴![]() 或2,
或2,
∵∠PCB>45°,
∴![]() ,
,
∴点P的坐标为(1,4);
(3)如图3中,作RM⊥DQ于M,连接EM,DH交AB于N.设D(n,![]() ).
).
∵D、E两点关于抛物线对称轴对称,点P的坐标(1,4),抛物线对称轴为![]() ,
,
∴PQ∥DE∥![]() 轴,DQ⊥
轴,DQ⊥![]() 轴,
轴,
∴Q(n,4),
∴DE=![]() ,DQ=
,DQ=![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠EDQ=∠EDH=90°,
∴△EDQ∽△HDE,
∴∠DEQ=∠EHD,
∵∠DEQ+∠EQD=90°,
∴∠EHD+∠EQD=90°,
∴∠HEQ=90°,
∵∠REH+∠RMH=180°,
∴E、H、M、R四点共圆,
∴∠ERH=∠EMH,
∴tan∠ERH=tan∠EMD=![]() ,
,
∴DM=![]() ,
,
∴QM=DQ-DM=![]() ,
,
∵RM⊥DQ,
∴RM∥DE,
∴![]() ,即
,即 ,
,
∴RM=![]() ,
,
∴点R的坐标为![]() ,
,
即![]() ,
,
把点R坐标代入![]() 得到:
得到:
![]() ,
,
解得:![]() ,
,
∴点D的坐标为(![]() ,
,![]() ).
).