题目内容
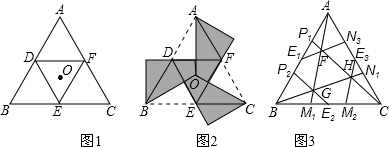
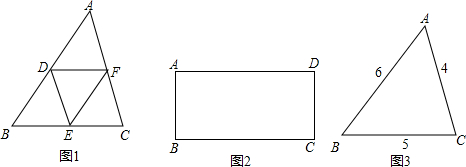
定义:如果一个图形经过分割,能分为4个与自身相似的图形,我们称它为“能四阶自相似分割图形”.如图1,任意△ABC取各边的中点D、E、F,连接DE、EF、DF,分得的△ADF、△BDE、△DEF、△CEF显然都与△ABC相似,则任意△ABC是“能四阶自相似分割图形”.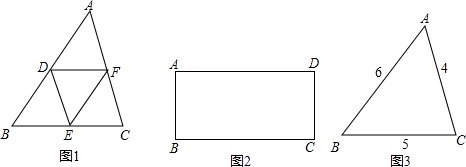
(1)小明发现:任意矩形ABCD(如图2)也是“能四阶自相似分割图形”.请你利用尺规作图作出分割线.(保留作图痕迹,不要求写作法)
(2)同组的小华思考后提出:能不能设计一种方案,将任意△ABC分割成四个与△ABC相似的小三角形,且其中至少有两个小三角形的相似比不为1?为了研究方便,小华取AB=6,AC=4,BC=5,(如图3)并成功地设计出了分法.请你完成小华的分法,并简单地说明理由.
分析:(1)作AD的中垂线MN、AB的中垂线PQ即可,分成的四个矩形和原来的矩形相似.
(2)在BC上取点D,过点D作DE∥AB交AC于点E,过点D作DF∥AC交AB于点F,就可以将任意△ABC分割成四个与△ABC相似的小三角形,且其中至少有两个小三角形的相似比不为1.
(2)在BC上取点D,过点D作DE∥AB交AC于点E,过点D作DF∥AC交AB于点F,就可以将任意△ABC分割成四个与△ABC相似的小三角形,且其中至少有两个小三角形的相似比不为1.
解答: 解:(1)如图2,作AD的中垂线MN、AB的中垂线PQ即可,分得的四个矩形与原矩形相似.(2分)
解:(1)如图2,作AD的中垂线MN、AB的中垂线PQ即可,分得的四个矩形与原矩形相似.(2分)
(2)如图3,在BC上取点D,过点D作DE∥AB交AC于点E,过点D作DF∥AC交AB于点F,易证:△CDE∽△DBF∽△CBA,
四边形AEDF为平行四边形,
设CE=x,则AE=4-x,
∵△CDE∽△CBA,可得
=
,∴DE=
x,
∴AF=DE=
x,(6分)
如果:△AEF∽△ABC,可得
=
,∴CE=
,
∴AF=
,CD=
.(8分)
(其他类似方法同样给分)
 解:(1)如图2,作AD的中垂线MN、AB的中垂线PQ即可,分得的四个矩形与原矩形相似.(2分)
解:(1)如图2,作AD的中垂线MN、AB的中垂线PQ即可,分得的四个矩形与原矩形相似.(2分)(2)如图3,在BC上取点D,过点D作DE∥AB交AC于点E,过点D作DF∥AC交AB于点F,易证:△CDE∽△DBF∽△CBA,
四边形AEDF为平行四边形,
设CE=x,则AE=4-x,
∵△CDE∽△CBA,可得
| CE |
| CA |
| DE |
| AB |
| 3 |
| 2 |
∴AF=DE=
| 3 |
| 2 |
如果:△AEF∽△ABC,可得
| AF |
| CA |
| AE |
| AB |
| 16 |
| 13 |
∴AF=
| 24 |
| 13 |
| 20 |
| 13 |
(其他类似方法同样给分)
点评:本题考查了相似三角形的判定和性质,相似三角形的对应边成比例以及应用与设计作图的知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目