题目内容
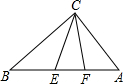 如图,在直角的直角顶点C作斜边AB的三等分点的连线CE、CF,已知CE=sinα,CF=cosα(α为锐角),则边AB的长是多少?
如图,在直角的直角顶点C作斜边AB的三等分点的连线CE、CF,已知CE=sinα,CF=cosα(α为锐角),则边AB的长是多少?
分析:作EM⊥BC,FN⊥AC,构造直角三角形,然后利用勾股定理和三角函数的平方关系解题.
解答: 解:设AC=b,BC=a.分别过E、F作EM⊥BC,FN⊥AC,垂足为M,N.
解:设AC=b,BC=a.分别过E、F作EM⊥BC,FN⊥AC,垂足为M,N.
∵BE=EF=FA,
则EM=
a,FN=
a,
CM=
b,
CN=
b,
在Rt△CEM中,
(
a)2+(
b)2=sin2α,
在Rt△CFN中,
(
a)2+(
b)2=cos2α,
∴
a2+
b2=1,a2+b2=
,
故AB=
=
.
 解:设AC=b,BC=a.分别过E、F作EM⊥BC,FN⊥AC,垂足为M,N.
解:设AC=b,BC=a.分别过E、F作EM⊥BC,FN⊥AC,垂足为M,N.∵BE=EF=FA,
则EM=
| 2 |
| 3 |
| 1 |
| 3 |
CM=
| 1 |
| 3 |
CN=
| 2 |
| 3 |
在Rt△CEM中,
(
| 2 |
| 3 |
| 1 |
| 3 |
在Rt△CFN中,
(
| 1 |
| 3 |
| 2 |
| 3 |
∴
| 5 |
| 9 |
| 5 |
| 9 |
| 9 |
| 5 |
故AB=
| a2+b2 |
3
| ||
| 5 |
点评:此题考查了三角函数的平方关系和定义,作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
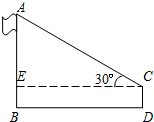 在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据
在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据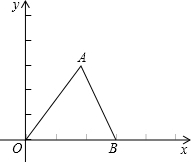 如图,在平面直角坐标系中,已知:△ABC的三个顶点的坐标分别是A(4,6)、B(0,0)、C(6,0).
如图,在平面直角坐标系中,已知:△ABC的三个顶点的坐标分别是A(4,6)、B(0,0)、C(6,0). 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.