题目内容
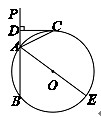
已知：如图，直线
交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作
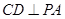于D.
1.求证：CD为⊙O的切线；
2.若DC+DA=6，⊙O的直径为10，求AB的长.
1.见解析。
2.AB=6
解析:（1）证明：连接OC，
∵点C在⊙O上，OA=OC，
∴
∵
，
∴
，
.
∵AC平分∠PAE，
∴
……………………………………………………………………………1分
∴
又∵点C在⊙O上，OC为⊙O的半径，
∴CD为⊙O的切线. …………………………………………………………………………2分
（2）解:过O作
于点F，
∴
，
∴四边形OCDF为矩形，
∴
……………………………3分
∵DC+DA=6，设
,
∴
∵⊙O的直径为10，
∴
，
∴
.
在
中，
∵
即
化简得
，
解得
或x=9. ……………………………………………………………4分
∵
，
∴.
∵，
∴
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
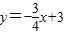交x轴于O1，交y轴于O2，⊙O2与x轴相切于O点，交直线O1O2于P点，以O1为圆心，O1P为半径的圆交x轴于A、B两点，PB交⊙O2于点F，⊙O1的弦BE=BO，EF的延长线交AB于D，连接PA、PO．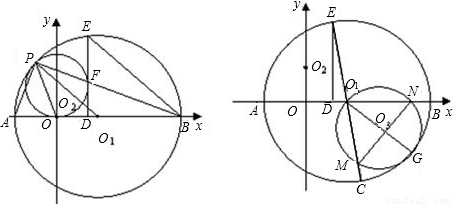
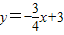交x轴于O1，交y轴于O2，⊙O2与x轴相切于O点，交直线O1O2于P点，以O1为圆心，O1P为半径的圆交x轴于A、B两点，PB交⊙O2于点F，⊙O1的弦BE=BO，EF的延长线交AB于D，连接PA、PO．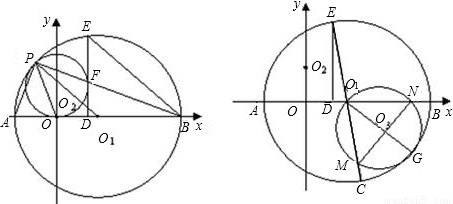
交x轴于O1，交y轴于O2，⊙O2与x轴相切于O点，交直线O1O2于P点，以O1为圆心，O1P为半径的圆交x轴于A、B两点，PB交⊙O2于点F，⊙O1的弦BE=BO，EF的延长线交AB于D，连接PA、PO．
交x轴于点B，交y轴于点C，点A为x轴正半轴上一点，AO=CO，△ABC的面积为12．