Question

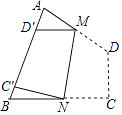
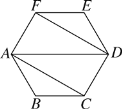
【题目】如图，六边形ABCDEF的内角都相等，∠DAB＝60°，AB＝DE，则下列结论：①AB∥DE；②EF∥AD∥BC；③AF＝CD；④四边形ACDF是平行四边形；⑤六边形ABCDEF既是中心对称图形，又是轴对称图形．其中成立的个数是(　　)

A. 2个 B. 3个 C. 4个 D. 5个

Answer 1

【答案】D

【解析】根据六边形ABCDEF的内角都相等，∠DAB=60°，平行线的判定，平行四边形的判定，中心对称图形的定义一一判断即可．

∵六边形ABCDEF的内角都相等，∴∠EFA=∠FED=∠FAB=∠ABC=120°．

∵∠DAB=60°，∴∠DAF=60°，∴∠EFA+∠DAF=180°，∠DAB+∠ABC=180°，∴AD∥EF∥CB，故②正确，∴∠FED+∠EDA=180°，∴∠EDA=∠ADC=60°，∴∠EDA=∠DAB，∴AB∥DE，故①正确．

∵∠FAD=∠EDA，∠CDA=∠BAD，EF∥AD∥BC，∴四边形EFAD，四边形BCDA是等腰梯形，∴AF=DE，AB=CD．

∵AB=DE，∴AF=CD，故③正确，连接CF与AD交于点O，连接DF、AE、DB、BE．

∵∠CDA=∠DAF，∴AF∥CD，AF=CD，∴四边形ACDF是平行四边形，故④正确，同法可证四边形AEDB是平行四边形，∴AD与CF，AD与BE互相平分，∴OF=OC，OE=OB，OA=OD，∴六边形ABCDEF是中心对称图形，且是轴对称，故⑤正确．

故选D．