题目内容
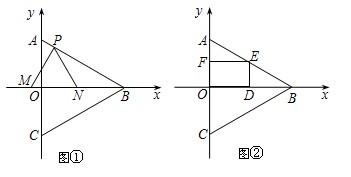
 如图所示,矩形ABCD中,AB=8,BC=6,P是线段BC上一点(P不与B重合),M是DB上一点,且BP=DM,设BP=x,△MBP的面积为y,则y与x之间的函数关系式为________.
如图所示,矩形ABCD中,AB=8,BC=6,P是线段BC上一点(P不与B重合),M是DB上一点,且BP=DM,设BP=x,△MBP的面积为y,则y与x之间的函数关系式为________.
y= x2+4x(0<x≤6)
x2+4x(0<x≤6)
分析:根据勾股定理可得BD=10,因为DM=x,所以BM=10-x,过点M作ME⊥BC于点E,可得到△BME∽△BDC,然后根据相似三角形的性质得到 =
= ,由此即可用x表示ME,最后根据三角形的面积公式即可确定函数关系式.
,由此即可用x表示ME,最后根据三角形的面积公式即可确定函数关系式.
解答: 解:∵AB=8,BC=6,
解:∵AB=8,BC=6,
∴CD=8,
∴BD=10,
∵DM=x,
∴BM=10-x,
如图,过点M作ME⊥BC于点E,
∴ME∥DC,
∴△BME∽△BDC,
∴ =
= ,
,
∴ME=8- x,
x,
而S△MBP= ×BP×ME,
×BP×ME,
∴y= x2+4x,P不与B重合,那么x>0,可与点C重合,那么x≤6.
x2+4x,P不与B重合,那么x>0,可与点C重合,那么x≤6.
故填空答案:y= x2+4x(0<x≤6).
x2+4x(0<x≤6).
点评:本题的难点是利用相似得到△MBP中BP边上的高ME的代数式,此题主要考查了利用相似三角形的性质确定函数关系式.
 x2+4x(0<x≤6)
x2+4x(0<x≤6)分析:根据勾股定理可得BD=10,因为DM=x,所以BM=10-x,过点M作ME⊥BC于点E,可得到△BME∽△BDC,然后根据相似三角形的性质得到
 =
= ,由此即可用x表示ME,最后根据三角形的面积公式即可确定函数关系式.
,由此即可用x表示ME,最后根据三角形的面积公式即可确定函数关系式.解答:
 解:∵AB=8,BC=6,
解:∵AB=8,BC=6,∴CD=8,
∴BD=10,
∵DM=x,
∴BM=10-x,
如图,过点M作ME⊥BC于点E,
∴ME∥DC,
∴△BME∽△BDC,
∴
 =
= ,
,∴ME=8-
 x,
x,而S△MBP=
 ×BP×ME,
×BP×ME,∴y=
 x2+4x,P不与B重合,那么x>0,可与点C重合,那么x≤6.
x2+4x,P不与B重合,那么x>0,可与点C重合,那么x≤6.故填空答案:y=
 x2+4x(0<x≤6).
x2+4x(0<x≤6).点评:本题的难点是利用相似得到△MBP中BP边上的高ME的代数式,此题主要考查了利用相似三角形的性质确定函数关系式.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
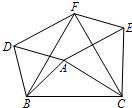 18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
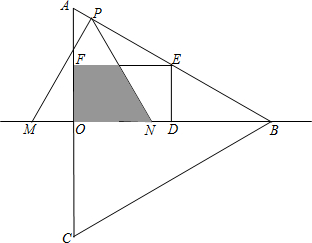 边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.
边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上. (2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是( )
(2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是( )