题目内容
以线段AB为直径作一个半圆,圆心为O,C是半圆周上的点,且OC2=AC•BC,则∠CAB=________.
75°或15°
分析:根据直径所对的圆周角是直角求得∠ACB=90°;又有三角形的面积公式:面积=底×高、面积= absinC,及已知条件OC2=AC•BC,求得sin∠AOC=
absinC,及已知条件OC2=AC•BC,求得sin∠AOC= ;分类讨论:当∠AOC=30°时,∠COB=180°-30°=150°;当∠AOC=150°时,∠COB=180°-150°=30°;由同弧所对的圆周角是圆心角的一半求得∠CAB=
;分类讨论:当∠AOC=30°时,∠COB=180°-30°=150°;当∠AOC=150°时,∠COB=180°-150°=30°;由同弧所对的圆周角是圆心角的一半求得∠CAB= ∠COB.
∠COB.
解答: 解:∵AB为直径,C是半圆周上的点,
解:∵AB为直径,C是半圆周上的点,
∴∠ACB=90°,0A=OB=OC,
∴S△ABC= AC•BC,
AC•BC,
S△AOC= S△ABC;
S△ABC;
又∵OC2=AC•BC,
∴ OC2=2•
OC2=2• OC2sin∠AOC,
OC2sin∠AOC,
∴sin∠AOC= ;
;
当∠AOC=30°时,∠COB=180°-30°=150°
∠CAB= ∠COB=75°(同弧所对的圆周角是圆心角的一半);
∠COB=75°(同弧所对的圆周角是圆心角的一半);
当∠AOC=150°时,∠COB=180°-150°=30°
∠CAB= ∠COB=15°(同弧所对的圆周角是圆心角的一半).
∠COB=15°(同弧所对的圆周角是圆心角的一半).
故答案为:75°或15°.
点评:本题综合考查了圆周角定理、三角形的面积公式及特殊角的三角函数值.解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解.
分析:根据直径所对的圆周角是直角求得∠ACB=90°;又有三角形的面积公式:面积=底×高、面积=
 absinC,及已知条件OC2=AC•BC,求得sin∠AOC=
absinC,及已知条件OC2=AC•BC,求得sin∠AOC= ;分类讨论:当∠AOC=30°时,∠COB=180°-30°=150°;当∠AOC=150°时,∠COB=180°-150°=30°;由同弧所对的圆周角是圆心角的一半求得∠CAB=
;分类讨论:当∠AOC=30°时,∠COB=180°-30°=150°;当∠AOC=150°时,∠COB=180°-150°=30°;由同弧所对的圆周角是圆心角的一半求得∠CAB= ∠COB.
∠COB.解答:
 解:∵AB为直径,C是半圆周上的点,
解:∵AB为直径,C是半圆周上的点,∴∠ACB=90°,0A=OB=OC,
∴S△ABC=
 AC•BC,
AC•BC,S△AOC=
 S△ABC;
S△ABC;又∵OC2=AC•BC,
∴
 OC2=2•
OC2=2• OC2sin∠AOC,
OC2sin∠AOC,∴sin∠AOC=
 ;
;当∠AOC=30°时,∠COB=180°-30°=150°
∠CAB=
 ∠COB=75°(同弧所对的圆周角是圆心角的一半);
∠COB=75°(同弧所对的圆周角是圆心角的一半);当∠AOC=150°时,∠COB=180°-150°=30°
∠CAB=
 ∠COB=15°(同弧所对的圆周角是圆心角的一半).
∠COB=15°(同弧所对的圆周角是圆心角的一半).故答案为:75°或15°.
点评:本题综合考查了圆周角定理、三角形的面积公式及特殊角的三角函数值.解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解.

练习册系列答案
相关题目
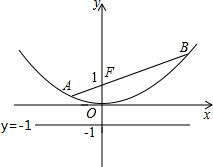 如图,已知点F的坐标为(0,1),过点F作一条直线与抛物线y=
如图,已知点F的坐标为(0,1),过点F作一条直线与抛物线y= 交于点A和点B,若以线段AB为直径作圆,则该圆与直线y=-1的位置关系是 .
交于点A和点B,若以线段AB为直径作圆,则该圆与直线y=-1的位置关系是 .
 交于点A和点B,若以线段AB为直径作圆,则该圆与直线y=-1的位置关系是 .
交于点A和点B,若以线段AB为直径作圆,则该圆与直线y=-1的位置关系是 .
 交于点A和点B,若以线段AB为直径作圆,则该圆与直线y=-1的位置关系是 .
交于点A和点B,若以线段AB为直径作圆,则该圆与直线y=-1的位置关系是 .
 交于点A和点B,若以线段AB为直径作圆,则该圆与直线y=-1的位置关系是 .
交于点A和点B,若以线段AB为直径作圆,则该圆与直线y=-1的位置关系是 .