题目内容
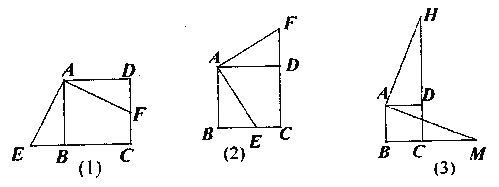
【题目】(1)观察发现:四边形ABCD是正方形,点E是直线BC上的动点,连结AE,过点A作AF⊥AE交直线CD于F.当点E位于点B的左侧时,如图(1).观察线段AB.BE.CF之间有何数量关系?请直接写出线段AB.BE.CF之间的数量关系.
(2)拓展探究:当点E位于点B的右侧时,如图(2),线段AB.BE.CF之间有何数量关系?并说明理由.
(3)迁移应用:如图(3),正方形ABCD的边长为2cm时,线段CM=3cm,直接写出线段CH的长.
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)7cm
,理由见解析;(3)7cm
【解析】试题分析: ![]() 观察图形,即可得到三条线段之间的数量关系.
观察图形,即可得到三条线段之间的数量关系.
![]() 证明
证明![]() 即可得到三条线段之间的数量关系.
即可得到三条线段之间的数量关系.
![]() 利用
利用![]() 中的结论.
中的结论.
试题解析:
(1)![]() .
.
(2) ![]() ;
;
理由如下: ![]() 是正方形
是正方形
∴![]() ,
,![]()
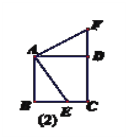
∵![]() ,
,
![]()
∴![]() ,
,
在![]() 和
和![]() 中
中
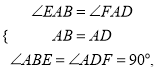
![]()
∴![]() ,
,
∴![]() .
.
(3) ![]()

练习册系列答案
相关题目

