题目内容
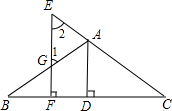 已知:如图,AD⊥BC于D,EF⊥BC于F,EF交AB于G,交CA延长线于E,
已知:如图,AD⊥BC于D,EF⊥BC于F,EF交AB于G,交CA延长线于E,
且∠1=∠2.
求证:AD平分∠BAC,填写“分析”和“证明”中的空白.
分析:要证明AD平分∠BAC,
只要证明∠________=∠________,
而已知∠1=∠2,所以应联想这两个角分别和∠1、∠2的关系,
由已知AD⊥BC、EF⊥BC可推出
________∥________,这时可以得到∠1=________,∠2=________.
从而不难得到结论AD平分∠BAC.
证明:∵AD⊥BC,EF⊥BC(已知)
∴________∥________(________)
∴________=________(两直线平行,内错角相等.)
________=________(两直线平行,同位角相等.)
∵________(已知)
∴________,
即AD平分∠BAC(________)
BAD CAD AD EF ∠BAD ∠CAD AD EF 同一平面内,垂直于同一条直线的两条直线平行 ∠1 ∠BAD ∠2 ∠DAC ∠1=∠2 ∠BAD=∠DAC 角平分线的定义
分析:根据平行线的性质与判定定理,即同一平面内,垂直于同一条直线的两条直线平行,分别得出答案即可.
解答:根据平行线的性质与判定定理,故答案为:
BAD,CAD,
AD,EF,
AD,EF,同一平面内,垂直于同一条直线的两条直线平行;
∠1,∠BAD,
∠2,∠DAC,
∠1=∠2,
∠BAD=∠DAC,
角平分线的定义.
点评:此题主要考查了平行线的性质与判定,此题有分析过程,可以很好的培养同学们的分析的思维,得出AD∥EF是解决问题的关键.
分析:根据平行线的性质与判定定理,即同一平面内,垂直于同一条直线的两条直线平行,分别得出答案即可.
解答:根据平行线的性质与判定定理,故答案为:
BAD,CAD,
AD,EF,
AD,EF,同一平面内,垂直于同一条直线的两条直线平行;
∠1,∠BAD,
∠2,∠DAC,
∠1=∠2,
∠BAD=∠DAC,
角平分线的定义.
点评:此题主要考查了平行线的性质与判定,此题有分析过程,可以很好的培养同学们的分析的思维,得出AD∥EF是解决问题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 27、已知:如图,AD∥BC,ED∥BF,且AF=CE.
27、已知:如图,AD∥BC,ED∥BF,且AF=CE. 25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.
25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.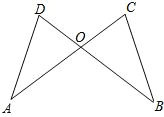 已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.
已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.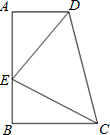 已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC.
已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC. 根据题意填空:
根据题意填空: