题目内容
【题目】如图,已知二次函数![]() 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.
(1)求二次函数![]() 的解析式;
的解析式;
(2)将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,直线y=m(m>0)交
,直线y=m(m>0)交![]() 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,![]() 、
、![]() 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与![]() 、
、![]() 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与![]() 、
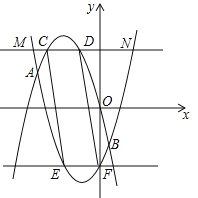
、![]() 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)根据待定系数法即可解决问题.
(2)先求出抛物线y2的顶点坐标,再求出其解析式,利用方程组以及根与系数关系即可求出MN.
(3)用类似(2)的方法,分别求出CD、EF即可解决问题.
试题解析:(1)∵二次函数![]() 过(﹣2,4),(﹣4,4)两点,∴
过(﹣2,4),(﹣4,4)两点,∴![]() ,解得:
,解得: ,∴二次函数
,∴二次函数![]() 的解析式
的解析式![]() .
.
(2)∵![]() =
=![]() ,∴顶点坐标(﹣3,
,∴顶点坐标(﹣3,![]() ),∵将
),∵将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,∴抛物线
,∴抛物线![]() 的顶点坐标(﹣1,
的顶点坐标(﹣1,![]() ),∴抛物线
),∴抛物线![]() 为
为![]() ,由
,由 ,消去y整理得到
,消去y整理得到![]() ,设
,设![]() ,
,![]() 是它的两个根,则MN=
是它的两个根,则MN=![]() =
=![]() =
=![]() ;
;
(3)由 ,消去y整理得到
,消去y整理得到![]() ,设两个根为
,设两个根为![]() ,
,![]() ,则CD=
,则CD=![]() =
=![]() =
=![]() ,由
,由 ,消去y得到
,消去y得到![]() ,设两个根为
,设两个根为![]() ,
,![]() ,则EF=
,则EF=![]() =
=![]() =
=![]() ,∴EF=CD,EF∥CD,∴四边形CEFD是平行四边形.
,∴EF=CD,EF∥CD,∴四边形CEFD是平行四边形.


练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目