Question

如图，点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点（其中P、Q不与端点重合），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ、CP交于点M，则在P、Q运动的过程中，下列结论：⑴BP=CM；⑵△ABQ≌△CAP；⑶∠CMQ的度数始终等于60°；⑷当第秒或第秒时，△PBQ为直角三角形．其中正确的结论有（ ）

A．1个 B．2个 C．3个 D．4个

 

Answer 1

A．

【解析】

试题分析：A、在等边△ABC中，AB=BC．

∵点P、Q的速度都为1cm/s，

∴AP=PQ，

∴BP=CQ．

只有当CM=CQ时，BP=CM．故本选项错误；

B、∵△ABC是等边三角形

∴∠ABQ=∠CAP，AB=CA，

又∵点P、Q运动速度相同，

∴AP=BQ，

在△ABQ与△CAP中，

∵，

∴△ABQ≌△CAP（SAS）．

故本选项正确；

C、点P、Q在运动的过程中，∠QMC不变．

理由：∵△ABQ≌△CAP，

∴∠BAQ=∠ACP，

∵∠QMC=∠ACP+∠MAC，

∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°．故本选项正确；

D、设时间为t秒，则AP=BQ=tcm，PB=（4-t）cm，

当∠PQB=90°时，

∵∠B=60°，

∴PB=2BQ，即4-t=2t，t= ，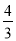

当∠BPQ=90°时，

∵∠B=60°，

∴BQ=2BP，得t=2（4-t），t=，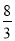

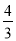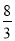∴当第秒或第秒时，△PBQ为直角三角形．故本选项正确．

故选A．

考点：1.全等三角形的判定与性质；2.等边三角形的性质．