题目内容
 在某次足球训练中,一队员在距离球门12米处挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图).现有四个结论:①a-b>0;②a<-
在某次足球训练中,一队员在距离球门12米处挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图).现有四个结论:①a-b>0;②a<-| 1 |
| 60 |
| 1 |
| 60 |
| A、①③ | B、①④ | C、②③ | D、②④ |
分析:根据二次函数的性质得出a,b的符号,即可得出①正确性,再利用图上点的坐标得出a,b关系,即可得出答案.
解答:解:∵a<0,ab异号,b>0,
∴a-b<0,故此选项①错误;
首先可以确定抛物线过点(12,0),(0,2.4)代入得:
144a+12b+c=0,c=2.4
得,b=-12a-
,而b=-12a-
>0,
解得:a<-
,故此选项②正确;
∴综上所述,故此选项③错误;
另外,抛物线的对称轴的横坐标小于6 即-
<6,
a<0 则b<-12a 另外,
由图象可以看出ax2+bx+c=0有两个根,且满足x1+x2>0,
则-
>0,而a<0,所以b>0
因此 0<b<-12a,故此选项④正确;
故选:D.
∴a-b<0,故此选项①错误;
首先可以确定抛物线过点(12,0),(0,2.4)代入得:
144a+12b+c=0,c=2.4
得,b=-12a-
| 1 |
| 5 |
| 1 |
| 5 |
解得:a<-
| 1 |
| 60 |
∴综上所述,故此选项③错误;
另外,抛物线的对称轴的横坐标小于6 即-
| b |
| 2a |
a<0 则b<-12a 另外,
由图象可以看出ax2+bx+c=0有两个根,且满足x1+x2>0,
则-
| b |
| a |
因此 0<b<-12a,故此选项④正确;
故选:D.
点评:此题主要考查了二次函数的性质,根据题意得出图象上的点进而得出a,b的关系是解决问题的关键.

练习册系列答案
相关题目
 为了备战2008奥运会,中国足球队在某次训练中,一队员在距离球门12米处的挑射,正好从2.4米高(球门横梁底侧高)入网.若足球运行的路线是抛物线y=ax2+bx+c(如图所示),则下列结论正确的是( )
为了备战2008奥运会,中国足球队在某次训练中,一队员在距离球门12米处的挑射,正好从2.4米高(球门横梁底侧高)入网.若足球运行的路线是抛物线y=ax2+bx+c(如图所示),则下列结论正确的是( )①a<-
| 1 |
| 60 |
| 1 |
| 60 |
| A、①③ | B、①④ | C、②③ | D、②④ |
 为了备战世界杯,中国足球队在某次训练中,一队员在距离球门12m处的挑射正好射中了2.4m高的球门横梁,若足球运行的路线是抛物线y=ax2+bx+c(如图所示)则下列结论:①a<-
为了备战世界杯,中国足球队在某次训练中,一队员在距离球门12m处的挑射正好射中了2.4m高的球门横梁,若足球运行的路线是抛物线y=ax2+bx+c(如图所示)则下列结论:①a<- 在某次足球训练中,一队员在距离球门12米处挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图).现有四个结论:①a-b>0;②a<-
在某次足球训练中,一队员在距离球门12米处挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图).现有四个结论:①a-b>0;②a<-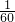 ;③-
;③- ;③-
;③- <a<0;④0<b<-12a.其中正确的结论是( )
<a<0;④0<b<-12a.其中正确的结论是( )