题目内容
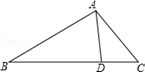
如图,△ABC中,∠B=90°,AB=5,BC=12,将△ABC沿DE折叠,使点C落在AB边上的 处,并且
处,并且 ∥BC,则CD的长是( ).
∥BC,则CD的长是( ).
A. | B.6 | C. | D. |
A.
解析试题分析:根据题意可知,四边形ECDC’是菱形.先设CD=x,再根据比例线段可求出CD的长.
∵将△ABC沿DE折叠,使点C落在AB上的C’处,
∴△DC’E≌△DCE,
∴∠C’ED=∠CED,∠C’DE=∠CDE,
∵C’D∥BC,
∴∠DEC=∠C’DE,
∴∠C’ED=∠CED=∠C’DE=∠CDE,
∴DC’=EC’=EC=CD,
∴四边形C’ECD是菱形,
又∵C’D∥BC,
∴ ,
,
∵
设CD=x,
∴
∴
故选A.
考点: 1.勾股定理;2.翻折变换(折叠问题).

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
如图,在△ 中,点
中,点 分别在
分别在 边上,
边上, ∥
∥ ,若
,若 ,
, ,则
,则 等于
等于
A. | B. | C. | D. |
如图,在 中,DE∥BC,且AD:AB=2:3,则DE:BC的值为
中,DE∥BC,且AD:AB=2:3,则DE:BC的值为
A. | B. | C. | D.2 |
如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A.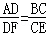 | B. | C. | D.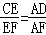 |
如果 ,那么下列比例式变形正确的是
,那么下列比例式变形正确的是
A. | B. | C. | D. |
如图,在△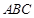 中,点
中,点 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且 ∥
∥ ,若
,若 ,
,  ,
, 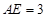 ,则
,则 的长为( )
的长为( )
| A.3 | B.6 | C.9 | D.12 |
如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有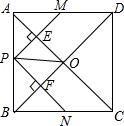
| A.5个 | B.4个 | C.3个 | D.2个 |
如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
| A.(2,4) | B.(-1,-2) |
| C.(-2,-4) | D.(-2,-1) |