题目内容
 如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,若△ABC的面积是12,则涂黑部分的面积是
如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,若△ABC的面积是12,则涂黑部分的面积是3
3
.分析:根据三角形的中线把三角形分成两个面积相等的三角形解答.
解答:解:∵点D是BC的中点,
∴S△ABD=S△ACD=
S△ABC=
×12=6,
∵点E是AD的中点,
∴S△BDE=
S△ABD=
×6=3,
S△CDE=
S△ACD=
×6=3,
∴S△BCE=S△BDE+S△CDE=3+3=6,
∵点F是CE的中点,
∴S△BEF=
S△BCE=
×6=3.
故答案为:3.
∴S△ABD=S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∵点E是AD的中点,
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BCE=S△BDE+S△CDE=3+3=6,
∵点F是CE的中点,
∴S△BEF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:3.
点评:本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,在一块如图所示的三角形余料上裁剪下一个正方形,如果△ABC为直角三角形,且∠ACB=90°,AC=4,BC=3,正方形的四个顶点D、E、F、G分别在三角形的三条边上.求正方形的边长.
如图,在一块如图所示的三角形余料上裁剪下一个正方形,如果△ABC为直角三角形,且∠ACB=90°,AC=4,BC=3,正方形的四个顶点D、E、F、G分别在三角形的三条边上.求正方形的边长.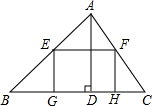 (2011•德阳)如图,有一块△ABC材料,BC=10,高AD=6,把它加工成一个矩形零件,使矩形的一边GH在BC上,其余两个顶点E,F分别在AB,AC上,那么矩形EFHG的周长l的取值范围是( )
(2011•德阳)如图,有一块△ABC材料,BC=10,高AD=6,把它加工成一个矩形零件,使矩形的一边GH在BC上,其余两个顶点E,F分别在AB,AC上,那么矩形EFHG的周长l的取值范围是( )
