题目内容
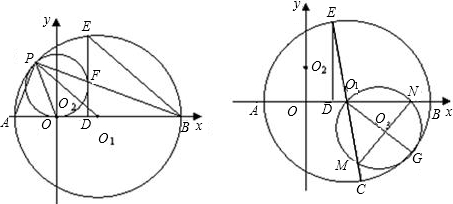
在平面直角坐标系xOy中,△AOB的位置如图所示,已知∠AOB= 90°,∠A=60°,点A的坐标为(-
90°,∠A=60°,点A的坐标为(-
,1).
求:(1)点B的坐标;
(2)图象经过A、O、B三点的二次函数的解析式和这个函数图象的顶点坐标.
 90°,∠A=60°,点A的坐标为(-
90°,∠A=60°,点A的坐标为(-| 3 |
求:(1)点B的坐标;
(2)图象经过A、O、B三点的二次函数的解析式和这个函数图象的顶点坐标.
(1)如图,过A作AC⊥OD于C,过B作BD⊥DO与D,
∵点A的坐标为(-
,1),
∴AO=2,
∵∠AOB=90°,∠BAO=60°,
∴tan∠BAO=
,
∴BO=2
,
∵
=
,
∴∠AOC=30°,
∠BOD=60°,
∴点B的坐标为(
,3);
(2)设这个二次函数的解析式为y=ax2+bx+c(a≠0),(1分)
∵二次函数的图象经过A、O、B三点,
∴
,
解得:
,
所以二次函数的解析式为y=
x2+
x,
∴函数图象的顶点坐标为(-
,-
).

∵点A的坐标为(-
| 3 |
∴AO=2,
∵∠AOB=90°,∠BAO=60°,
∴tan∠BAO=
| OB |
| OA |
∴BO=2
| 3 |
∵
| AC |
| OA |
| 1 |
| 2 |
∴∠AOC=30°,
∠BOD=60°,
∴点B的坐标为(
| 3 |
(2)设这个二次函数的解析式为y=ax2+bx+c(a≠0),(1分)
∵二次函数的图象经过A、O、B三点,
∴
|
解得:
|
所以二次函数的解析式为y=
| 2 |
| 3 |
| ||
| 3 |
∴函数图象的顶点坐标为(-
| ||
| 4 |
| 1 |
| 8 |


练习册系列答案
相关题目

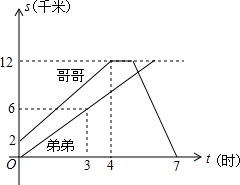
 间x(分)的关系式为y=kx+400,当周华回到家时,刘明刚好到达体育场.
间x(分)的关系式为y=kx+400,当周华回到家时,刘明刚好到达体育场.