题目内容
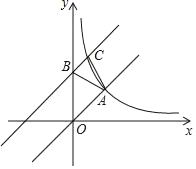
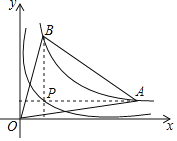
【题目】如图，点P为函数y＝
（x＞0）图象上一点，过点P作x轴、y轴的平行线，分别与函数y＝
（x＞0）的图象交于点A、B，则△AOB的面积为_____．
【答案】24
【解析】
作AD⊥x轴于D，设PB⊥x轴于E，设P(m，
)，则A(5m，)，B(m，
)，由点A、B在函数y＝
(x＞0)的图象上，可得S△OBE＝S△OAD，根据S△AOB＝S四边形ABOD﹣S△OAD＝S四边形ABOD﹣S△OBE＝S梯形ABED，利用面积公式进行求解即可.
作AD⊥x轴于D，设PB⊥x轴于E，
∵点P为函数y＝
(x＞0)图象上一点，过点P作x轴、y轴的平行线，
∴设P(m，)，则A(5m，)，B(m，)，
∵点A、B在函数y＝(x＞0)的图象上，
∴S△OBE＝S△OAD，
∵S△AOB＝S四边形ABOD﹣S△OAD＝S四边形ABOD﹣S△OBE＝S梯形ABED，
∴S△AOB＝
(+)(5m﹣m)＝24，
故答案为24．
练习册系列答案
相关题目
