Question

【题目】已知二次函数的部分图象如图，顶点是．

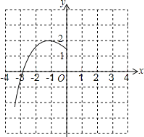
（1）求二次函数的解析式；

（2）若抛物线上两点、的横坐标满足，则________；（用“”、“”或“”填空）

（3）观察图象，直接写出当时，的取值范围．

Answer 1

【答案】（1）y=；（2）；（3）

【解析】

（1）设二次函数顶点式解析式为y=a（x+1）2+2，然后把点（﹣3，0）代入求出a的值，即可得解；

（2）根据x＜﹣1时，y随x的增大而减小解答；

（3）根据二次函数的对称性求出抛物线与x轴的另一交点，然后写出x轴上方部分的x的取值范围即可．

（1）∵顶点是（﹣1，2），∴设二次函数顶点式解析式为y=a（x+1）2+2，由图可知，函数图象经过点（﹣3，0），∴a（﹣3+1）2+2=0，解得：a=﹣，∴二次函数的解析式为y=﹣（x+1）2+2，即y=；

（2）∵a=﹣＜0，二次函数图象对称轴为直线x=﹣1，∴x＞﹣1时，y随x的增大而减小，∴﹣1＜x1＜x2时，y1＞y2．

故答案为：＞；

（3）∵函数图象经过（﹣3，0），对称轴为直线x=﹣1，∴二次函数与x轴的另一交点坐标为（1，0），∴y＞0时，x的取值范围﹣3＜x＜1．