题目内容
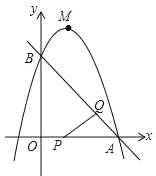
【题目】如图,抛物线![]() 与
与![]() 轴的负半轴相交于点
轴的负半轴相交于点![]() ,将抛物线
,将抛物线![]() 平移得到抛物线
平移得到抛物线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,且
,且![]() .
.
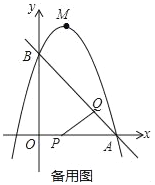
(1)求点![]() 的坐标;
的坐标;
(2)写出一种将抛物线![]() 平移到抛物线
平移到抛物线![]() 的方法;
的方法;
(3)在![]() 轴上找点
轴上找点![]() ,使得
,使得![]() 的值最小,求点
的值最小,求点![]() 的坐标.
的坐标.
【答案】(1)A(-2,0),B(3,5),C(8,10);(2)先将![]() 向右平移5个单位,再向上平移5个单位得到
向右平移5个单位,再向上平移5个单位得到![]() ;(3)P(0,
;(3)P(0,![]() ).
).
【解析】
(1)y=0,即求A;AB=BC,得![]() ,求出直线AB的解析式与二次函数求交点,利用根与系数的关系求m的值,从而确定B与C的坐标;
,求出直线AB的解析式与二次函数求交点,利用根与系数的关系求m的值,从而确定B与C的坐标;
(2)抛物线平移前后a的值不变,由点B(3,5),C(8,10)在抛物线y=x2+bx+c上,确定抛物线解析式,从而得到平移过程;
(3)作点B关于y轴的对称点B',连接CB'与y轴的交点即为P,求出直线B'C的直线解析式的解析式与y轴交点即为P;
解:(1)M1:y=x2-4与x轴的负半轴相交于点A,

∴A(-2,0),
∵AB=BC,C(8,m),
∴![]() ,
,
设AB直线解析式为y=kx+b


![]() ,
,
∵y=x2-4与![]() 相交于点A和B,
相交于点A和B,
![]()
![]()
∴m=10,
∴B(3,5),C(8,10);
(2)∵抛物线M1平移得到抛物线M2,
∴a=1,
∵B(3,5),C(8,10)在抛物线y=x2+bx+c上,
![]()
![]()
∴y=x2-10+26=(x-5)2+1,
由M1平移得到抛物线M2先向右平移5个单位长度,再向上平移5个单位长度;
(3)作点B关于y轴的对称点B',连接CB'与y轴的交点即为P,
∴B'(-3,5),
设直线B'C的直线解析式为y=mx+n,
![]()

![]()
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目