题目内容
【题目】阅读材料，并完成相应任务.
2000多年来，人们对勾股定理的证明颇感兴趣，不但因为这个定理重要、基本，还因为这个定理贴近人们的生活实际，所以很多人都探讨、研究它的证明，新的证法不断出现.
下面的图形是传说中毕达哥拉斯的证明图形：
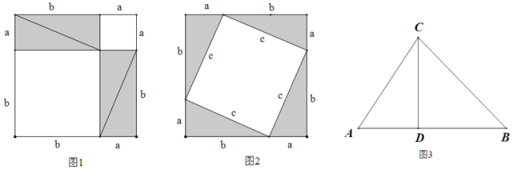
证明：①在图1中，∵
4个直角三角形的面积+两个正方形的面积
=4× + + .
②在图2中，∵
4个直角三角形的面积+正方形的面积
=4× + .
∴4× + + =4× + .
整理得：
∴ .
任务：（1）将材料中的空缺部分补充完整；
（2）如图3，在△ABC中，∠A=60°,∠ACB=75°，CD⊥AB，AC=4，求BC的长.
【答案】（1）
，，，
；（2）BC=
【解析】
（1）根据图形的特点及完全平方公式即可验证勾股定理；
（2）根据直角三角形中的特殊角与勾股定理即可求解.
（1）①在图1中，∵
4个直角三角形的面积+两个正方形的面积
=4×
+
+
.
②在图2中，∵
4个直角三角形的面积+正方形的面积
=4×+
.
∴4×++ =4×+ .
整理得：
∴ .
故填：，，
，
（2）∵CD⊥AB
∴∠ADC=∠BDC=90°
∵∠A=60°
∴∠ACD=30°
∵AC=4
∴AD=2
在Rt△ACD中
CD=
又∵∠ACB=75°
∴∠DCB=∠ACB-∠ACD=45°
∴∠B=45°
∴ BD=CD=
在Rt△BCD中
BC=
练习册系列答案
阅读快车系列答案
相关题目
