题目内容
已知Rt△ABC中，∠C=90°，AC=8cm，BC=6cm．则其内心和外心之间的距离是
- A.10cm
- B.5cm
- C.
cm - D.2cm
C
分析：如图，根据勾股定理即可求解．
解答：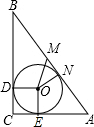
解：如图，在Rt△ABC，∠C=90°，AC=8cm，BC=6cm，
∴AB=10cm，
∴AM为外接圆半径．
设Rt△ABC的内切圆的半径为r，则OD=OE=r，∠C=90°，
∵四边形OECD是正方形，
∴CE=CD=r，AE=AN=6-r，BD=BN=8-r，
即8-r+6-r=10，
解得r=2cm，
∴AN=4cm；
在Rt△OMN中，
MN=AM-AN=1cm，
OM=cm．
故选C．
点评：此题考查了直角三角形的外心与内心概念，及内切圆的性质．
分析：如图，根据勾股定理即可求解．
解答：
解：如图，在Rt△ABC，∠C=90°，AC=8cm，BC=6cm，∴AB=10cm，
∴AM为外接圆半径．
设Rt△ABC的内切圆的半径为r，则OD=OE=r，∠C=90°，
∵四边形OECD是正方形，
∴CE=CD=r，AE=AN=6-r，BD=BN=8-r，
即8-r+6-r=10，
解得r=2cm，
∴AN=4cm；
在Rt△OMN中，
MN=AM-AN=1cm，
OM=
cm．故选C．
点评：此题考查了直角三角形的外心与内心概念，及内切圆的性质．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
如图，已知Rt△ABC中，∠ACB=90°，AC=4，BC=3，以AB边所在的直线为轴，将△ABC旋转一周，则所得几何体的表面积是（ ）A、
| ||
| B、24π | ||
C、
| ||
| D、12π |
22、如图所示，已知Rt△ABC中，AB=AC，BD平分∠ABC，CE⊥BD交BD延长线于E，BA、CE延长线相交于F点．
10、如图，已知Rt△ABC中，∠C=90°∠A=36°，以C为圆心，CB为半径的圆交AB于P，则弧BP的度数是
已知Rt△ABC中，∠ACB=90°，CA=CB，点D在BC的延长线上，点E在AC上，且CD=CE，延长BE交AD于点F，求证：BF⊥AD．