题目内容
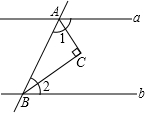 如图,直线a∥b,直线AB交a与b于A,B,CA平分∠1,CB平分∠2,求证:∠C=90°.
如图,直线a∥b,直线AB交a与b于A,B,CA平分∠1,CB平分∠2,求证:∠C=90°.
分析:由于a∥b,∠1,∠2是两个同侧内角,因此∠1+∠2=180°,那么
(∠1+∠2)=90°,过C点作直线l,使l∥a(或b)即可通过平行线的性质得到
∠1+
∠2与∠C相等,实现等角转移.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: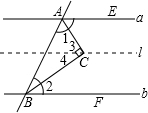 证明:过C点作直线l,使l∥a
证明:过C点作直线l,使l∥a
∵a∥b
∴b∥l
∴∠1+∠2=180°(同旁内角互补)
∵AC平分∠1,BC平分∠2
∴∠CAE=
∠1,∠CBF=
∠2
又∵∠3=∠CAE,∠4=∠CBF(内错角相等)
∴∠3+∠4=∠CAE+∠CBF=
(∠1+∠2)=90°
∴∠C=∠3+∠4=90°.
 证明:过C点作直线l,使l∥a
证明:过C点作直线l,使l∥a∵a∥b
∴b∥l
∴∠1+∠2=180°(同旁内角互补)
∵AC平分∠1,BC平分∠2
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠3=∠CAE,∠4=∠CBF(内错角相等)
∴∠3+∠4=∠CAE+∠CBF=
| 1 |
| 2 |
∴∠C=∠3+∠4=90°.
点评:本题考查平行线的性质和角平分线的性质.两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
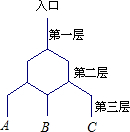 如图所示是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层,依此类推,现有一颗小弹子从第一层的通道里向下运动.并且小弹子落入每一条通道的可能性相同,则该小弹子从第三层通道的出口B脱出的概率为
如图所示是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层,依此类推,现有一颗小弹子从第一层的通道里向下运动.并且小弹子落入每一条通道的可能性相同,则该小弹子从第三层通道的出口B脱出的概率为