题目内容
如图1,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
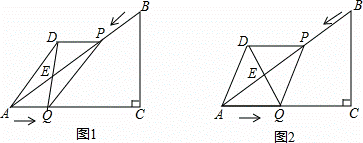
(1)用含有t的代数式表示AE= 5﹣t .
(2)当t为何值时,平行四边形AQPD为矩形.
(3)如图2,当t为何值时,平行四边形AQPD为菱形.
| 解:(1)∵Rt△ABC中,∠C=90°,AC=8cm,BC=6cm. ∴由勾股定理得:AB=10cm, ∵点P由B出发沿BA方向向点A匀速运动,速度均为2cm/s, ∴BP=2tcm, ∴AP=AB﹣BP=10﹣2t, ∵四边形AQPD为平行四边形, ∴AE= (2)当▱AQPD是矩形时,PQ⊥AC, ∴PQ∥BC, ∴△APQ∽△ABC ∴ 即 解之 t= ∴当t= (3)当▱AQPD是菱形时,DQ⊥AP, 则 COS∠BAC= 即 解之 t= ∴当t= |

 期末冲刺100分创新金卷完全试卷系列答案
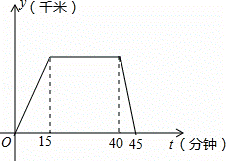
期末冲刺100分创新金卷完全试卷系列答案如图是王老师去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法正确的是( )
|
| A. | 王老师去时所用的时间少于回家的时间 |
|
| B. | 王老师在公园锻炼了40分钟 |
|
| C. | 王老师去时走上坡路,回家时走下坡路 |
|
| D. | 王老师去时速度比回家时的速度慢 |
下列图形中,既是轴对称图形又是中心对称图形的是( )
|
| A. | 矩形 | B. | 平行四边形 | C. | 等腰梯形 | D. | 等腰三角形 |
国庆节期间,电器市场火爆.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
| 类 别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1 800 | 1 500 |
| 售价(元/台) | 2 000 | 1 600 |
计划购进电视机和洗衣机共100台,商店最多可筹集资金161 800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获 得利润最多?并求出最多利润.(利润=售价-进价)
得利润最多?并求出最多利润.(利润=售价-进价)
 =5﹣t;
=5﹣t;


 =
=


 是反比例函数
是反比例函数 图像上的点,若
图像上的点,若 ,
, B、
B、
 D、
D、
 和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是
和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是