题目内容
(2007•潍坊)2006年潍坊市学业水平考试数学学科的考试成绩以等级公布.以县(市)为单位将所有考生成绩按由高到低分为A,B,C,D,E五个等级,五个等级所占比例依次为15%,20%,30%,20%,15%.小明所在学习小组随机抽查本学校2006年毕业学生,了解参加学业水平考试的考生数学成绩(等级)情况,统计如下表:| 成绩(等级) | A | B | C | D | E |
| 人数 | 16 | 20 | 24 | 12 | 8 |
(2)根据小明所在学习小组的调查,估计2006年全校1320名参加数学考试的学生中,数学成绩(等级)为A,B等的考生各有多少人?
(3)根据抽查结果,请你对小明所在学校参加2006年学业水平考试的数学成绩在全县(市)内的情况发表自己的看法.
【答案】分析:(1)根据扇形所对圆心角的度数与百分比的关系是:圆心角的度数=百分比×360度计算各等的对应的扇形的圆心角;
(2)根据扇形统计图中,各部分的数量=总体×所占百分比求解;
(3)可以得出:A等、B等人数都比全市A等、B等平均人数多,
C等人数与全市C等平均人数持平,
D等、E等人数都比全市D等、E等平均人数少.
解答:解:(1)由题意得,抽到的总人数为:16+20+24+12+8=80人,
表示A的扇形的圆心角=360°× =72°,
=72°,
表示B的扇形的圆心角=360°× =90°,
=90°,
表示C的扇形的圆心角=360°× =108°,
=108°,
表示D的扇形的圆心角=360°× =54°,
=54°,
表示E的扇形的圆心角=360°× =36°,
=36°,
如图:
(2)A等人数为20%×1320=264(人)
B等人数为25%×1320=330(人)
(3)A等、B等人数都比全市A等、B等平均人数多,
C等人数与全市C等平均人数持平,
D等、E等人数都比全市D等、E等平均人数少.
点评:扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚的表示出各部分数量同总数之间的关系.
(2)根据扇形统计图中,各部分的数量=总体×所占百分比求解;
(3)可以得出:A等、B等人数都比全市A等、B等平均人数多,
C等人数与全市C等平均人数持平,
D等、E等人数都比全市D等、E等平均人数少.
解答:解:(1)由题意得,抽到的总人数为:16+20+24+12+8=80人,
表示A的扇形的圆心角=360°×
 =72°,
=72°,表示B的扇形的圆心角=360°×
 =90°,
=90°,
表示C的扇形的圆心角=360°×
 =108°,
=108°,表示D的扇形的圆心角=360°×
 =54°,
=54°,表示E的扇形的圆心角=360°×
 =36°,
=36°,如图:
(2)A等人数为20%×1320=264(人)
B等人数为25%×1320=330(人)
(3)A等、B等人数都比全市A等、B等平均人数多,
C等人数与全市C等平均人数持平,
D等、E等人数都比全市D等、E等平均人数少.
点评:扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚的表示出各部分数量同总数之间的关系.

练习册系列答案
相关题目
(2007•潍坊)蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间x(月份)与市场售价p(元/千克)的关系如下表:
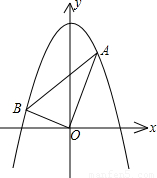
这种蔬菜每千克的种植成本y(元/千克)与上市时间x(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

| 上市时间x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| 市场销售p(元/千克) | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

(2007•潍坊)蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间x(月份)与市场售价p(元/千克)的关系如下表:
这种蔬菜每千克的种植成本y(元/千克)与上市时间x(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

| 上市时间x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| 市场销售p(元/千克) | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

(2007•潍坊)蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间x(月份)与市场售价p(元/千克)的关系如下表:
这种蔬菜每千克的种植成本y(元/千克)与上市时间x(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

| 上市时间x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| 市场销售p(元/千克) | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

(2007•潍坊)蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间x(月份)与市场售价p(元/千克)的关系如下表:
这种蔬菜每千克的种植成本y(元/千克)与上市时间x(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

| 上市时间x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| 市场销售p(元/千克) | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)