题目内容
设x1、x2是关于x的方程x2-（m-1）x-m=0（m≠0）的两个根，且满足
+
=-
，求m的值．
解：∵△=（m+1）2≥0，
∴对于任意实数m，方程恒有两个实数根x1，x2．
又∵x1+x2=m-1，x1x2=-m，且m≠0，
∴+=-，
∴
=-，
∴
=-，
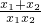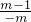∴3m-3=2m
∴m=3．
分析：本题是对根的判别式与根与系数关系的综合考查，因为方程有两个实数根，所以△=b2-4ac≥0，求出m的取值范围，然后根据+=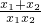，即可得到关于m的方程然后求解．
点评：命题立意：考查一元二次方程根与系数的关系及其应用．
∴对于任意实数m，方程恒有两个实数根x1，x2．
又∵x1+x2=m-1，x1x2=-m，且m≠0，
∴
+=-，∴
=-，∴
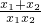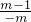=-，∴3m-3=2m
∴m=3．
分析：本题是对根的判别式与根与系数关系的综合考查，因为方程有两个实数根，所以△=b2-4ac≥0，求出m的取值范围，然后根据
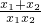+=，即可得到关于m的方程然后求解．点评：命题立意：考查一元二次方程根与系数的关系及其应用．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
设x1，x2是关于x的一元二次方程x2+x+n-2=mx的两个实数根，且x1＜0，x2-3x1＜0，则（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|