题目内容
在△ABC中,∠ACB=90°,∠ABC=15°,AC=1,则BC的长为________.
2
分析:本题中直角三角形的角不是特殊角,故过A作AD交BC于D,使∠BAD=15°,根据三角形内角和定理可求出∠DAC及∠ADC的度数,再由特殊角的三角函数值及勾股定理求解即可.
解答: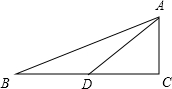 解:过A作AD交BC于D,使∠BAD=15°,
解:过A作AD交BC于D,使∠BAD=15°,
∵△ABC中.∠ACB=90°,∠ABC=15°,
∴∠BAC=75°,
∴∠DAC=∠BAC-∠BAD=75°-15°=60°,
∴∠ADC=90°-∠DAC=90°-60°=30°,
∴AC=AD,
又∵∠ABC=∠BAD=15°
∴BD=AD,
∵AC=1,
∴AD=BD=2,
DC= ,
,
∴BC=2+ ,
,
故答案为2+ .
.
点评:本题考查了勾股定理在直角三角形中的应用,解本题的关键是正确的运用勾股定理,确定AB为斜边.

分析:本题中直角三角形的角不是特殊角,故过A作AD交BC于D,使∠BAD=15°,根据三角形内角和定理可求出∠DAC及∠ADC的度数,再由特殊角的三角函数值及勾股定理求解即可.
解答:
 解:过A作AD交BC于D,使∠BAD=15°,
解:过A作AD交BC于D,使∠BAD=15°,∵△ABC中.∠ACB=90°,∠ABC=15°,
∴∠BAC=75°,
∴∠DAC=∠BAC-∠BAD=75°-15°=60°,
∴∠ADC=90°-∠DAC=90°-60°=30°,
∴AC=AD,
又∵∠ABC=∠BAD=15°
∴BD=AD,
∵AC=1,
∴AD=BD=2,
DC=
 ,
,∴BC=2+
 ,
,故答案为2+
 .
.点评:本题考查了勾股定理在直角三角形中的应用,解本题的关键是正确的运用勾股定理,确定AB为斜边.

练习册系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
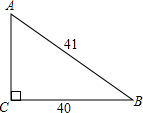 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=