题目内容
如图，P是等边三角形ABC内的一点，若将△PAC绕点A逆时针旋转到△P′AB，则∠PAP′的度数为
- A.30°
- B.45°
- C.60°
- D.90°
C
分析：根据旋转的性质，找出∠PAP′=∠BAC，根据等边三角形的性质，即可解答．
解答：
解：如图，根据旋转的性质得，
∠PAP′=∠BAC，
∵△ABC是等边三角形，
∴∠BAC=60°，
∴∠PAP′=60°；
故选C．
点评：本题主要考查了旋转的性质和等边三角形的性质，知道对应点与旋转中心所连线段的夹角等于旋转角，是解答本题的关键．
分析：根据旋转的性质，找出∠PAP′=∠BAC，根据等边三角形的性质，即可解答．
解答：
解：如图，根据旋转的性质得，∠PAP′=∠BAC，
∵△ABC是等边三角形，
∴∠BAC=60°，
∴∠PAP′=60°；
故选C．
点评：本题主要考查了旋转的性质和等边三角形的性质，知道对应点与旋转中心所连线段的夹角等于旋转角，是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，△ABC是等边三角形纸片，沿EF翻折，使点A落在BC边上的D点，设∠AEF=a，AE=x，AF=y．
（2012•历下区一模）如图，△ABC是等边三角形，△DEF是边长为7的等边三角形，点B与点E重合，点A、B、（E）、F在同一条直线上，将△ABC沿E→F方向平移至点A与点F重合时停止，设点B、E之间的距离为x，△ABC与△DEF重叠部分的面积为y，则能大致反映y与x之间函数关系的图象是（ ）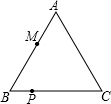
（2013•海淀区一模）如图，△ABC是等边三角形，AB=6厘米，点P从点B出发，沿BC以每秒1厘米的速度运动到点C停止；同时点M从点B出发，沿折线BA-AC以每秒3厘米的速度运动到点C停止．如果其中一个点停止运动，则另一个点也停止运动．设点P的运动时间为t秒，P、M两点之间的距离为y厘米，则表示y与t的函数关系的图象大致是（ ）
如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．
如图，△ABC是等边三角形，D是AB边上的一点，以CD为边作等边三角形CDE，使点E、A在直线DC的同侧，连结AE．