题目内容
已知平面直角坐标系中,抛物线y=-x2+4x与x轴交于点A(x1,0),x1>0,对称轴为直线l,点P(m,n)为抛物线上一点,且在第四象限,点P关于直线l对称点为E,点E关于x轴的对称点为F,若四边形OPAF的面积为20,求m、n的值.
考点:抛物线与x轴的交点
专题:
分析:首先根据抛物线的对称轴方程求出E点的坐标,进而可得到F点的坐标,由此可求出PF的长,即可判断出四边形OAPF的形状,然后根据其面积求出n的值,再代入抛物线的解析式中即可求出m的值.
解答:解:∵抛物线y=-x2+4x,
∴抛物线的对称轴为x=2,
∴点P(m,n)关于直线x=2的对称点坐标为点E(4-m,n),
∴点E关于y轴对称点为点F坐标为(m-4,n),
∴FP=OA=4,即FP、OA平行且相等,
∴四边形OAPF是平行四边形;
即S=OA•|n|=20,即|n|=5;
∵点P为第四象限的点,
∴n<0,
∴n=-5;
代入抛物线方程得m=-1(舍去)或m=5,
故m=5,n=-5.
∴抛物线的对称轴为x=2,
∴点P(m,n)关于直线x=2的对称点坐标为点E(4-m,n),
∴点E关于y轴对称点为点F坐标为(m-4,n),
∴FP=OA=4,即FP、OA平行且相等,
∴四边形OAPF是平行四边形;
即S=OA•|n|=20,即|n|=5;
∵点P为第四象限的点,
∴n<0,
∴n=-5;
代入抛物线方程得m=-1(舍去)或m=5,
故m=5,n=-5.
点评:此题主要考查二次函数的性质,坐标轴公式,顶点公式,此题是一道综合题,注意第二问难度比较大;

练习册系列答案
相关题目
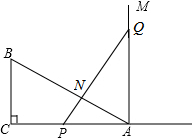 如图所示,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线上运动.问:
如图所示,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线上运动.问: