题目内容
在?ABCD中，E、F分别是AB、CD的中点，连接AF、CE．请你猜想：线段AF与线段EC有怎样的数量关系？并对你的猜想加以证明．
【答案】分析：由在?ABCD中，E、F分别是AB、CD的中点，利用SAS即可判定：△BEC≌△DFA，利用全等三角形的性质即可得到AF=CE．
解答：解：猜想：AF=CE，理由如下：
∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，∠B=∠D，
∵E、F分别是AB、CD的中点，
∴BE=
AB，DF=
CD，
∵在△BEC和△DFA中，
，
∴△BEC≌△DFA（SAS），
∴AF=CE．
点评：此题考查了平行四边形的性质、全等三角形的判定与性质，此题难度适中，注意掌握数形结合思想的应用．
解答：解：猜想：AF=CE，理由如下：
∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，∠B=∠D，
∵E、F分别是AB、CD的中点，
∴BE=
AB，DF=CD，∵在△BEC和△DFA中，
，∴△BEC≌△DFA（SAS），
∴AF=CE．
点评：此题考查了平行四边形的性质、全等三角形的判定与性质，此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
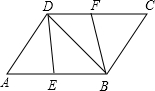如图，在?ABCD中，E、F分别为边AB、CD的中点，连接DE、BF、BD．
如图，在?ABCD中，EF∥AB，MN∥BC，MN与EF交于点O，且O点在对角线上，图中面积相等的四边形有（ ）
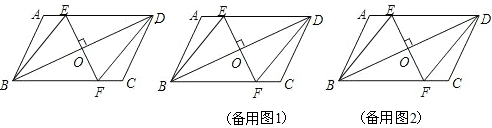
如图，在?ABCD中，点E在边BC上，点F在BC的延长线上，且BE=CF．