Question

20．如图，若△ABC的周长为1，它的3条中位线组成一个新的三角形，记作△A₁B₁C₁，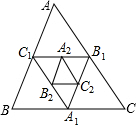
△A₁B₁C₁的3条中位线又组成一个新的三角形，记作△A₂B₂C₂ （如图所示），…，以此类推，求△A₂₀₁₇B₂₀₁₇C₂₀₁₇的周长是（$\frac{1}{2}$）²⁰¹⁷．

Answer 1

分析 根据三角形中位线定理求出△A₁B₁C₁的周长，根据规律解答．

解答 解：∵B₁C₁、A₁C₁、A₁B₁是△A₁B₁C₁的3条中位线，
∴B₁C₁、=$\frac{1}{2}$BC，A₁C₁=$\frac{1}{2}$AC，A₁B₁=$\frac{1}{2}$AB，
∴△A₁B₁C₁的周长=$\frac{1}{2}$，
同理△A₂B₂C₂，的周长=（$\frac{1}{2}$）²，
以此类推，△A₂₀₁₇B₂₀₁₇C₂₀₁₇的周长为（$\frac{1}{2}$）²⁰¹⁷，
故答案为：（$\frac{1}{2}$）²⁰¹⁷．

点评 本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．